All published articles of this journal are available on ScienceDirect.
Non-uniform Compression of Magnetic Resonance Brain Images Using Edge-based Active Contours Driven by Maximum Entropy Threshold
Abstract
Introduction
As digital imaging data are growing exponentially, compression of medical images is a critical issue for efficient storage and reliable transmission. As a result, researchers are continuously exploring methods for reducing the size of medical images further.
Methods
To further improve the compression methods, this paper proposes the maximum entropy-based threshold incorporated into the edge-based active contour method to automate the initialization of the curve for accurate extraction of the diagnostic or pathologically significant parts from unevenly illuminated Magnetic Resonance (MR) brain images. The images are then segmented into informative and background parts, which are further subjected to high-bit-rate and low-bit-rate compressions, respectively. This non-uniform compression results in an improvement in compression rate while preserving the quality of the diagnostic parts of the images.
Results and Discussion
The evaluation was performed on the dataset of MR brain images, and empirical analysis confirmed that the proposed method is able to outperform other existing methods in terms of segmentation and compression metrics.
Conclusion
The mathematical results of the proposed method indicate that the extracted area of the informative parts was similar to the object of interest in ground truth images. This accurate demarcation of the informative parts results in an improvement in compression rate without compromising the quality of the informative parts.
1. INTRODUCTION
In the field of image processing, the size of raw medical images is comparatively large due to high resolution, requiring large memory space to store the images in their raw form. With advancements in healthcare infrastructure, the production of medical images is rising exponentially, thereby necessitating more storage. Segmentation-based compression techniques play a key role in clinical applications that enable physicians to increase the precision of diagnostic procedures. The precise demarcation of the region of interest is required for effective compression of different medical images to reduce the transmission bandwidth and enhance the storage space. Therefore, compression of medical images of large size, such as MR images and CT scans, is essential to maximize the storage efficiency and reduce the bandwidth required for transmission. The maintenance of records of these medical images is essential for enhancing clinical proficiency, ensuring accurate diagnosis, and improving treatment outcomes. However, it requires substantial disk space to store these high-resolution images [1].
A medical image consists of numerous pixels, and theoretically, it is represented as a matrix of pixel intensity values. Generally, these pixel values are repetitive for the images, especially in medical images, and therefore, by exploiting this pixel redundancy, compression of the image is achieved. The image compression minimizes the number of bits required to code the pixel values. The compression techniques may be categorized into two types: lossless compression and lossy compression. In lossless compression, the image or information is retrieved back by the receiver without any losses or in its original form. In contrast, lossy compression leads to some losses in the final information retrieved at the receiver end, but the compression rate achieved by lossy compression is much greater than in lossless compression.
A hybrid approach aims to harness the benefits of both techniques, where the informative part of the image is extracted using segmentation. The informative part refers to the part of the image that contains all the desired information needed for diagnosis [2]. Thus, to extract the informative part, an input image is subjected to segmentation, which splits the image into the foreground part (FG) and background part (BG). Then, the informative and background parts are processed through lossless and lossy compression, respectively, resulting in an increase in the overall compression rate without compromising the quality of the informative part of the image.
However, the manual extraction of the foreground part is prone to error and is a time-consuming process. Consequently, computer-aided processing has been developed to overcome this limitation. In image analysis, segmentation is carried out before compression. Segmentation techniques are further categorized based on their characteristics, like segmentation based on different thresholds, region-based segmentation, segmentation based on edge detection, segmentation based on the contours, segmentation based on different clustering techniques, recognition-based segmentation, and artificial intelligence-based segmentation [3]. Different segmentation techniques are applied to medical modalities based on their characteristics to extract the nearest match of the foreground part, similar to ground truth images. Active contour methods are widely used in the extraction of the informative parts due to their capacity to handle complex topological structures, but there are still many situations where this method fails to converge to the desired boundary, especially if image cluttering is high. To achieve better segmentation, a hybrid of two segmentation methods is proposed, where the active contour’s energy function is incorporated into the image information extracted by the maximum entropy threshold to reduce the effect of inhomogeneity.
After splitting the image into informative and background parts, lossless compression (high bit rate compression) is applied to the informative part, while lossy compression (low bit rate compression) is used for the background. This approach achieves a high compression ratio while preserving image quality. In a lossless compression algorithm, reconstructed images are similar to the original images, but the rate of compression is low. Some common lossless compression standards include Run-Length Encoding (RLE), Huffman Encoding, and the Joint Photographic Experts Group-Lossless Compression Standard (JPEG-LS). Common lossy image compression techniques include transform coding, vector quantization, and predictive coding, with transform-based coding techniques preferred due to their less computational complexity. Popular image compression techniques are based on different transformation techniques, such as Joint Photographic Experts Group (JPEG), which is based on Discrete Cosine Transform (DCT), and JPEG2000, which is based on wavelet transform [4]. Therefore, both compression techniques can be incorporated using segmentation to get a high compression rate and satisfactory visual quality of the informative part of the images.
2. RELATED WORK
In this section, some representative papers from the relevant literature are discussed to provide an overview of the development of compression methods, current issues, and challenges.
Arif et al. [5] introduced a lossless compression technique for efficient transmission of fluoroscopic images. Firstly, the informative part was extracted using appropriate shapes, and this part was further subjected to compression using the integrated lossless coding approach to increase the compression rate. The mathematical analysis demonstrated that the presented method increased the compression rate by a significant amount.
Nithila et al. [6] introduced a region-based active contour model integrated with fuzzy c-means (FCM) clustering for the segmentation of nodules in lung computed tomography. The Gaussian filtering with a new signed pressure force function (SBGF-new SPF) was applied for the reconstruction of parenchyma, and the clustering technique was employed to extract the nodule segmentation. This method reduced the error rate and also increased the similarity measure.
Pratondo et al. [7] incorporated edge stop functions into an edge-based active contours algorithm to extract the accurate object of interest in medical images having poorly defined boundaries of the objects. This presented work incorporated a gradient function and probability scores from the classification algorithm into the active contour method, and the mathematical evaluation indicated the improvement in Jaccard and similarity indexes.
Nasifoglu et al. [8] presented adaptive image compression (AIC) for the identification of multi-region hip fractures in various pelvic radiographs. This method detected three diagnostically relevant regions, ranked in the decreasing order of the significant details of the fracture. The first region captured the primary fracture indicators, while the subsequent regions contained progressively less critical information. According to the order of their priority, the first region was compressed using lossless Joint Photographic Expert Group (JPEG) compression at a high-quality factor, and the second and third regions were compressed at a low-quality factor. Experimental results showed that the compression ratio increased by six times without deteriorating the quality of the informative regions.
Renukalatha et al. [9] proposed an automated segmentation technique using statistical moments to extract the diagnostic regions of different noisy image modalities. Firstly, the statistical moment was used to estimate an optimal threshold value through the decomposition of the histogram of the different medical modalities. The database comprising different medical images was preprocessed to filter out the noisy images, and after that, the informative region was extracted from them. Finally, the performance of the presented method was compared with different techniques to verify its effectiveness.
Kasute et al. [10] introduced a segmentation-based compression technique in which the informative region was compressed using the wavelet-based Set Partitioning in Hierarchical Tree (SPIHT) method at a high bit rate, whereas the background region was compressed using the discrete wavelet transform (DWT) by quantizing the wavelet coefficients. Mathematical evaluation was carried out using various parameters like CR and PSNR. Results showed that as CR increased, PSNR decreased. Therefore, the visual quality of the image decreased as the compression ratio increased.
Liu et al. [11] proposed a binary fitting and Kullback–Leibler (KL) divergence-based model incorporated into the level set active contour framework to avoid the convergence failure of the energy function in accurately delineating object boundaries within images exhibiting intensity inhomogeneity. KL (Kullback-Leibler) divergence is the relative entropy minimizing the sum of divergence of different regions in an image for the optimal image segmentation, and incorporating the divergence model into the edge-based active contours for initialization avoids the convergence failure and early curve deformation. This method was tested on various synthetic and real images, and mathematical results indicated the improvement in segmentation while ensuring the accurate minimization of the curve towards the object of interest.
Vidhya et al. [12] presented a variational level set algorithm for the edge detection of the region of interest from the background. This region of interest was processed using a lossless compression algorithm, and the background part was processed using lossy compression to increase the overall compression rate. The mathematical evaluation of the presented work indicated an improvement in compression ratio.
Liu et al. [13] created a maximum entropy threshold method incorporated into the Firefly algorithm for the extraction of objects of interest from images. The empirical evaluation of the work was carried out using regional consistency in the image, and this method outperformed the maximum entropy threshold and basic firefly algorithm in terms of regional consistency and noise immunity.
Fang et al. [14] proposed a region-based fuzzy energy model incorporated into edge-based active contour methods to avoid an incorrect convergence of the energy function of active contours in noisy images. This region-based energy formulation was comprised of hybrid and local fuzzy information to guide the contours curve towards the boundary of the object. The mathematical results indicated that the proposed approach performed better than state-of-the-art active contour methods.
Sran et al. [15] developed a segmentation-based algorithm executed in two stages. In the first stage, a saliency model was integrated with Fuzzy C-Means (FCM) clustering for the extraction of the informative region. In the second stage, non-uniform compression was applied in parallel, where the informative and background regions were compressed at high and low bit rates, respectively, using an SPIHT encoder. The results showed a significant improvement in values of Compression Ratio (CR) and Peak Signal-to-Noise Ratio (PSNR).
Costea et al. [16] presented a novel segmentation for biomedical images. This method utilized a cellular neural network (CNN) for the detection of edges of objects of interest (microarray spots) and further employed this information into edge-based active contours for convergence of energy function to the boundaries of the target object. The coefficient of variation (CV) was used to evaluate the effectiveness of the presented method, and the results indicated the high efficiency of the proposed method.
Liu et al. [17] utilized the probability scores from the k-nearest neighbor classifier for the construction of the gradient information function, and this function was incorporated into the localized active contours method for the evolution of the curve to exact object boundaries. The experiment was conducted on cardiac MR images, and the results validated the accuracy and robustness of the proposed method.
Sreenivasulu et al. [18] suggested a region-growing technique for segmentation to separate the informative region from the background in an image. The diagnostically important region of the image was compressed in the transform domain using discrete wavelet transform (DWT), followed by lossless compression with a Huffman encoder. In contrast, the background region of the image was compressed using the SPIHT algorithm. This approach demonstrated better results as compared to PFCM in terms of both segmentation parameters and compression parameters.
Huang et al. [19] proposed a Fruitfly algorithm incorporated into the Otsu threshold to optimize the threshold for the accurate extraction of objects of interest in Lena and Cameraman images. The empirical evaluation indicated that this method outperformed the traditional Otsu threshold in terms of signal-to-noise ratio and peak signal-to-noise ratio, and execution time was also reduced by 50% from the conventional method.
Sran et al. [20] developed a model that identifies significant regions using a saliency-based approach, followed by the application of fuzzy thresholding to extract the informative part of the image. The performance of saliency-based segmentation (SBS) was compared with different clustering techniques, including kernel-based FCM clustering, mean shift clustering, and FCM clustering with the Level Set Method. The experimental results demonstrated that this method delivered better segmentation results even in noisy images.
Yang et al. [21] presented a bat algorithm utilized to optimize multilevel thresholding in which the Otsu and maximum entropy methods are used for the formulation of fitness functions. The evaluation of the presented technique was carried out using peak signal-to-noise ratio and structural similarity index, and the results indicated that the Otsu-based method was more robust in multilevel thresholding.
Singh et al. [22] proposed a hybrid technique by incorporating Otsu’s between-class variance method and maximum entropy method for multilevel thresholds. This technique aimed to determine the optimal threshold value for the accurate extraction of informative regions of an image. Moreover, various performance metrics like peak signal-to-noise ratio and standard deviation were used to evaluate the efficiency of the proposed method.
Ahmad Khan et al. [23] created the Dual-3DM3-AD model for the early detection of Alzheimer’s disease in different imaging modalities, such as MRI and PET scans. The pre-processing of the images involved noise reduction using the Quaternion Non-Local Means Denoising Algorithm, skull stripping through morphological function, and image enhancement via the Block Divider model. Further, an adapted mixed transformer with U-Net was implied for semantic segmentation, and then extracted features from both modalities were aggregated. The proposed approach outperformed similar existing models in multiclass Alzheimer’s diagnosis in terms of accuracy, F-measure, and sensitivity.
Kujur et al. [24] evaluated different CNN models for the brain tumor dataset and Alzheimer’s disease dataset using Principal Component Analysis (PCA) and without using PCA. The Alzheimer’s disease dataset demonstrated higher data complexity as compared to the brain tumor dataset, and the highest performance scores in the Alzheimer’s disease dataset and brain tumor dataset were 98.02% and 99.27%, respectively. This work concludes that the complexity of data plays an important role in the performance of CNN models.
Alqarafi et al. [25] proposed an efficient GC-T2 approach for the early detection of melanoma skin cancer. Several pre-processing techniques, like the median-enhanced Wiener filter and Enriched Manta-Ray optimization algorithm, were implied for noise reduction and image enhancement. Further, the lesion area was segmented by the incorporation of semantic segmentation and the DRL approach to reduce the complexity. The appropriate features were extracted using a multi-scale graph convolution network (M-GCN), and these feature maps were fused using a tri-level feature fusion module and integrated into the sigmoid function for the classification of melanoma. This model outperformed similar existing models in terms of accuracy, F1 score, and sensitivity.
Based on the findings of this review, the following inferences are being drawn about key issues and challenges still prevailing in the segmentation and compression techniques:
- Most of the existing compression algorithms have optimization issues because of their complex coding algorithms, thereby making them inefficient.
- Wavelet-based transformation techniques are preferred to achieve reliable transmission of images.
- Non-uniform image compression methods can not be implemented efficiently without perfect/accurate extraction of the informative region.
- The automated segmentation method is preferred over manual segmentation to avoid inaccurate extraction of the informative regions of the image.
- The contour-based segmentation techniques are stable as they can perform well on images having uneven characteristics or poor illumination.
- Any single method is not able to handle all image conditions efficiently due to the image’s varying characteristics, but the amalgamation of different segmentation methods can achieve a perfect extraction of the informative region.
3. PROPOSED METHODOLOGY
To achieve a good visual quality of the informative region and a high compression rate simultaneously, the segmentation technique should be able to extract the informative region similar to the ground truth images. Then, a high compression rate is achieved by applying transformation-based techniques to the informative region and background region, which are processed at a high bit rate and low bit rate, respectively. The variable bit rate results in the good quality of the informative region along with a large compression ratio, thereby outperforming the state-of-the-art methods.
3.1. Segmentation
In medical images, the informative regions are of uneven shapes, making their accurate detection and segmentation particularly challenging. The accurate segmentation requires that these uneven shapes be traced smoothly. Therefore, segmentation is being made more precise to ensure a higher compression ratio. Medical images like MRI brain detect abnormal growth of tissues, which enable the doctors to diagnose effectively, but extraction of false information can mislead the diagnostic process. Therefore, computer-aided detecting techniques facilitate the extraction of the abnormal growth of tissues or tumors in different medical modalities, which is primarily motivated by the necessity of preserving the quality of objects of interest during the transmission of the images.
Different thresholding techniques have been commonly used for the extraction of the informative regions or objects of interest. However, these methods do not work efficiently on multichannel images. In region-based segmentation, biased initialization of seed points may lead to inaccurate marking of informative regions. The clustering-based segmentation is sensitive to the noise present in the images; therefore, the extraction of the spatial information is required before clustering. Artificial intelligence methods require large datasets to train the networks, which is time-consuming. Active contour methods are widely used in the extraction of informative regions due to their capacity to handle complex topological structures, but there are still many situations where active contours fail to converge to the desired boundary, especially if image cluttering is high.
Therefore, to achieve better segmentation, this study incorporates an active contour energy function with image information extracted using the maximum entropy threshold to reduce the effect of inhomogeneity. The proposed method, called Maximum Entropy Threshold-driven Edge-Based Active Contours (MET-EBAC), enhances segmentation performance by integrating global image characteristics into the contour evolution process. The maximum entropy threshold determines the optimal threshold by maximizing the overall entropy, effectively distinguishing between regions of interest and background. The conventional edge-based active contour methods fail to converge to the exact object of interest in the case of noisy images, and sometimes, the deformation of the curve is stopped by the edges or noise. In contrast, the maximum entropy method proves to be useful for noisy images with uncertain boundaries for producing smooth segmentation. Therefore, the maximum entropy threshold is incorporated into the edge-based active contours for the initialization of the curve to improve the accuracy of the segmentation process.
Thus, the contribution of this segmentation work can be summarized as follows:
- Firstly, contrast is created between the informative and non-informative regions of the image by determining the optimum threshold using the maximum entropy method.
- Then, the Edge-Based Active Contours (EBAC) method is integrated into the curve initialized by the maximum entropy criterion to achieve convergence to the desired boundaries.
3.2. Conventional Edge-based Active Contours
Edge-based active contours define the shape of contours and deform the contours towards the boundary of informative regions under the influence of internal and external forces. This method works on the concept of energy minimization to track the outline of the object of interest in the image, where initial points are set manually. The energy function for the active contours is calculated using Eq. (1), which is as follows:
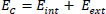 |
(1) |
Here, C is the curve initialized manually by a set of discrete points, and s is the arc length. The internal energy function Eint is represented by Eq. (2) as:
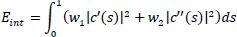 |
(2) |
Where, wi and w2 are weight parameters that control the rigidity and tension of the curve, and c' and c'' are first and second-order derivatives, respectively. The external energy function Eext controls the contour evolution depending on the image plane function Ω(x, y), and it is represented by the Eq. (3) as:
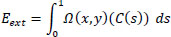 |
(3) |
The image information function is the image gradient function, which attracts the curve towards the boundaries of the object of interest, and it is represented by Eq. (4).
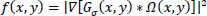 |
(4) |
Here, Gσ is the Gaussian filter, and ∇ denotes the gradient operator.
These initialized points move towards the optimum coordinates where the energy function converges to the minimum (Ec → min) and gives the final segmented image.
3.3. Modified Edge-based Active Contours Driven by Maximum Entropy Threshold
The maximum entropy criterion is utilized to determine the optimal threshold function, which is incorporated into edge-based active contours for automation of the initialization process to reduce the sensitivity of the algorithm towards noise in the images.
3.3.1. Maximum Entropy Threshold
This automated technique is used to determine the optimal threshold, implying the overall entropy to be maximized before processing the images for the edge-based active contours algorithm. This maximum entropy threshold criterion is used in the formulation of the objective function of the active contour method, where larger entropy values signify more uniformity in the image. The fitness function of the maximum entropy for bi-level thresholding (splitting into two classes) is given in Eq. (5) as:
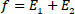 |
(5) |
The entropies of the two classes are calculated using Eq. (6), and the weights (total probabilities) of the two classes are measured using Eq. (7) as:
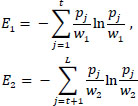 |
(6) |
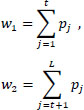 |
(7) |
Where, t is the threshold value, L is the intensity levels taken from grayscale images, and w1, w2, E1 and E2 are the probability distribution and entropies of class 1 and class 2, respectively. The optimal threshold function is given in Eq. (8) as [26]:
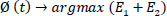 |
(8) |
3.4. Modified Edge-based Active Contour Method
The curve Ø (x, y, t) obtained from the maximum entropy threshold is incorporated into the objective function of edge-based active contours using the following Eq. (9):
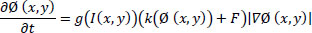 |
(9) |
Where g ← [0,1], and it is defined by the Eq. (10) as:
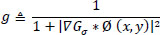 |
(10) |
Here, ‘g’ has smaller values at image boundaries compared to other regions of the image, and g(I(x, y))(k(Ø(x, y))+F) drives the contours in the normal direction and causes it to stop at the object boundaries, where g approaches zero. The curvature term k maintains the smoothness of the contours while constant force F speeds up the deformation process, thereby facilitating the evolution of contour towards the boundary of the object of interest by minimizing the enclosed area. The overall algorithm for the proposed segmentation is given below.
ALGORITHM OF PROPOSED SEGMENTATION
# I → Input Image
# Maximum Entropy Threshold (MET)
Step 1: w1 and w2 are the probability distributions of class 1 and class 2, respectively, and these are evaluated using Eq. (7).
Step 2: E1 and E2 are the probability entropies of class 1 and class 2, respectively, and these are evaluated using Eq. (6).
Step 3: The final fitness function of the maximum entropy for bi-level thresholding is calculated using Eq. (5).
Step 4: The optimal threshold function Ø (t) is achieved by maximizing the fitness function using Eq. (8).
# The curve or fitness function obtained from MET is incorporated into the edge-based active contour method.
# Edge-Based Active Contour Method (EBAC)
Step 5: The internal energy function controls the smoothness of the curve, and the external energy function leads the curve to the boundary until convergence is achieved. These functions are given in Eq. (11) as:
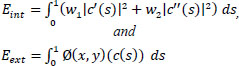 |
(11) |
# w1 and w2 are weight parameters that control the rigidity and tension of the curve, c' and c'' are first and second-order derivatives, respectively, and Ø(x, y) denotes the function defined on the image plane.
Step 6: Minimizing the contour length (motion motivated by energy minimization) speeds the deformation process and approaches zero when the contour reaches the object boundary (g vanishes) using Eqs. (9 and 10).
#Separating the Image in Two Parts
Step 7: Background Image = I- Foreground Image.
# These segmented parts are processed at different bit rates to achieve a non-uniform compression.
The final curve area extracted from the modified edge-based active contours is considered to be the informative region of the image, and these segmented parts are processed at different bit rates to achieve a non-uniform compression.
4. RESULTS AND DISCUSSION
4.1. Segmentation Evaluation Metrics
The efficacy of the segmentation is evaluated using the Jaccard similarity index or coefficient (J), the Dice coefficient (D), and the area of the foreground part. The Jaccard index is used for measuring the similarity and diversity of the sample sets (R, G), and it is calculated using Eq. (12).
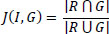 |
(12) |
The dice similarity coefficient is the spatial overlap index, which measures the degree of overlapping of the same sets, and it is given in Eq. (13).
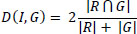 |
(13) |
Where R is the segmented informative region, and G is the ground image.
The percentage area of the foreground part extracted from the segmentation method is given in Eq. (14).
 |
(14) |
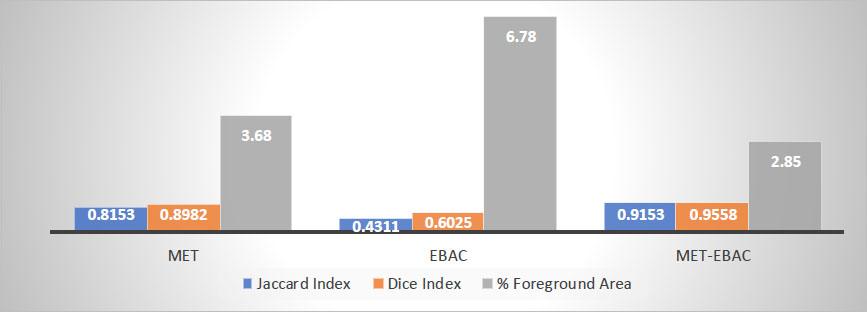
These parameters are evaluated for the informative regions extracted using different segmentation techniques. The average mathematical results obtained from maximum entropy threshold (MET), edge-based active contours (EBAC), and the proposed edge-based active contours incorporated with maximum entropy threshold (MET-EBAC) segmentation are summarized in Table 1.
Performance comparison of different segmentation methods.
| Metdods Parameters | MET Segmentation | EBAC Segmentation | MET-EBAC Segmentation |
| Jaccard index | 0.8153 | 0.4311 | 0.9153 |
| Dice index | 0.8982 | 0.6025 | 0.9558 |
| Foreground area (2.87%) | 3.68% | 6.78% | 2.85% |
Here, the percentage of the foreground area of the ground truth image is 2.87% of the total image area.
For better visualization and understanding, the result is presented in graphical form for different segmentation methods, as shown in Fig. (1).
The empirical outcomes shown in Table 1 indicate that the proposed approach of maximum entropy threshold incorporated into edge-based active contours outperforms maximum entropy threshold and conventional edge-based active contours in terms of different segmentation metrics, namely Jaccard index, dice index, and percentage of foreground area. The empirical evaluation of these indexes is performed using a dataset of 50 MRI brain images [27].
In terms of time complexity, the proposed approach outperforms the conventional edge-based active contour method, where the mean execution time is reduced by 2.56 seconds, and also the standard deviation of the proposed approach is less than the conventional method. Therefore, the proposed segmentation technique can meet the high computational demand in clinical applications. The statistical analysis of execution time illustrated in Table 2 shows the superiority of the proposed approach.
The statistical analysis supports that the proposed approach delineates the object of interest more efficiently due to the faster and less complex convergence of the contour. Therefore, the proposed approach can meet high computational demand, and it can be subjected to larger datasets for extraction of the object of interest.
| Methods Parameters | EBAC Segmentation | MET-EBAC Segmentation |
| Mean execution time (s) | 4.16 | 2.52 |
| Standard deviation of execution time (s) | 2.45 | 0.25 |
The qualitative analysis shown in Fig. (2) also validates the empirical analysis, and the binary mask extracted from the edge-based active contours driven by the maximum entropy threshold method is similar to the informative regions seen in the ground truth images. The binary mask extracted from the maximum entropy threshold (MET) shows undesirable demarcation of the object of interest, and conventional edge-based active contours fail to converge to the exact boundaries of the object of interest. On the other side, the proposed approach is able to extract a similar mask to the ground truth image. A qualitative comparison of the extraction of the object of interest using different algorithms is shown in the figure.
4.2. Compression
After extracting the informative and background regions of the image, the informative part is subjected to high bit-rate compression, and the background part is compressed to a low bit-rate compression using different compression methods, like Joint Photographic Experts Group (JPEG) and Set Partitioning in Hierarchical Tree (SPIHT). A flow chart of the proposed methodology is shown in Fig. (3).
The different transformation-based compression techniques used in the proposed methodology are JPEG (Joint Photographic Experts Group) and SPIHT (Set Partitioning in Hierarchical Trees) to validate the effectiveness of the proposed method. The JPEG compression standard is based on discrete cosine transformation (DCT), and SPIHT uses the discrete wavelet transformation (DWT) to transform the pixel values of the image into their respective transform coefficients. The informative and background regions of the images are processed separately at different bit rates to achieve a non-uniform compression, and finally, these parts are decoded by the JPEG and SPHIT decoders, followed by inverse transformations. These parts in the spatial domain are merged to obtain final output images at the receiver end.
4.2.1. JPEG
JPEG (Joint Photographic Experts Group) is the most popular image compression standard in the world. JPEG is considered both a lossy and lossless compression standard for digital images. The compression rate can be varied by making a trade-off between storage capacity and image quality, which means that the image may be subjected to a lower bit rate to achieve a higher compression rate at the cost of image quality.
Firstly, the input image is split into 8×8 non-overlapping blocks and then transformed into an array of high and low-frequency coefficients using discrete cosine transform (DCT), where low-frequency coefficients have maximum energy. After this, these coefficients are scanned in a zigzag manner, where they start from low-frequency coefficients and end up with high-frequency coefficients. The correlation between these coefficients is exploited through entropy coding of zigzag scanned coefficients, as shown in Fig. (4). The different compression rates can be achieved by quantizing the coefficients using different thresholds before scanning the coefficients [28].
4.2.2. SPIHT
SPIHT (Set Partitioning in Hierarchical Trees) is an image compression standard based on Discrete Wavelet Transform (DWT), which uses the principle of self-similarity across scale as an embedded zero wavelet. This method is used to code and decode the wavelet coefficients of the transformed image. This algorithm partitions the decomposed wavelet coefficients into significant and insignificant coefficients based on the function given in Eq. (15).
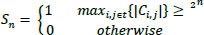 |
(15) |
Where n is log2Cmax, Sn is a significant set of coordinates, and Ci,j is the value of the coefficient at a particular coordinate (i, j).
This algorithm uses a sorting pass and a refinement pass, along with three sets of pixels: the list of insignificant pixels (LIP), the list of significant pixels (LSP), and the list of insignificant sets (LIS). This process of coefficient passing through these passes depends upon the desired compression rate, and a higher PSNR of the reconstructed image can be achieved by setting low thresholds [29].
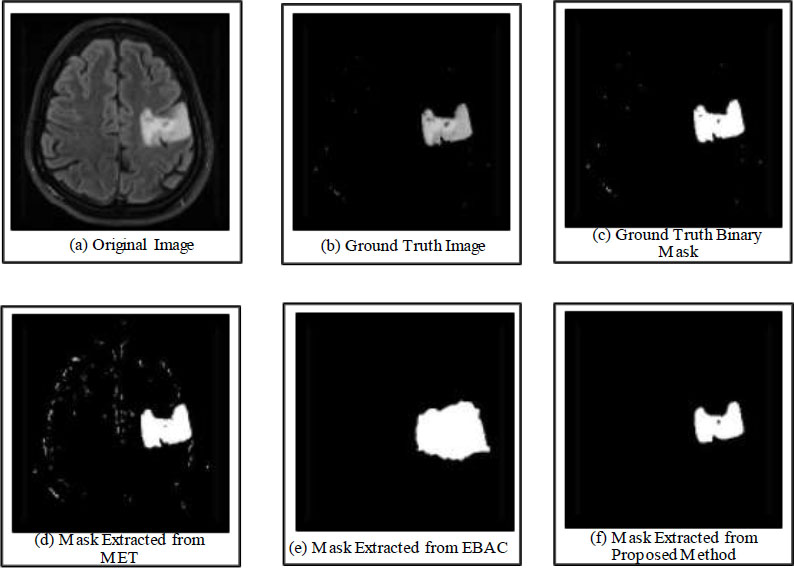
a) Original image, b) Ground truth image, c) Ground truth binary mask, d) Mask extracted from MET, e) Mask extracted from EBAC, f) Mask extracted from the Proposed method.
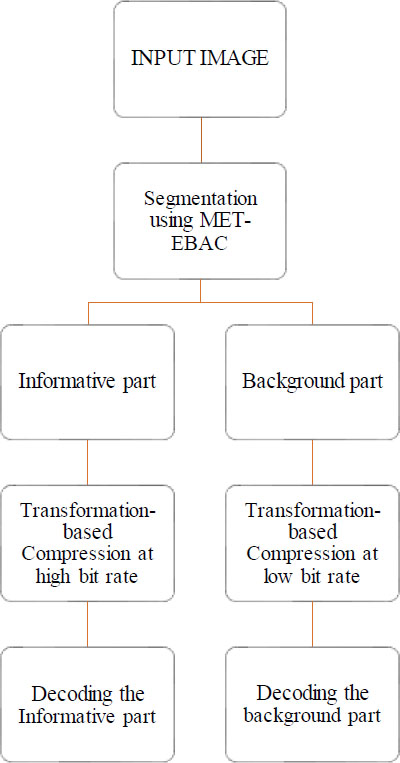
Flow chart of proposed methodology.
4.3. Proposed Compression Method
The MET-EBAC segmented parts are incorporated into the JPEG and SPIHT algorithms and processed at different bit rates. The informative region of the segmented image is compressed at higher values of bit rate to achieve a good quality informative part, and the background region is compressed at a low bit rate to achieve an overall high compression rate. After segmentation in the spatial domain, both parts of the image are processed simultaneously and transformed into DCT and DWT coefficients, and these transformed coefficients are subjected to JPEG and SPIHT encoders to attain a high compression rate while preserving the quality of the informative part. Finally, the compressed bitstream is decoded using JPEG and SPIHT decoders, resulting in the transformed coefficients. The inverse transformation of these coefficients allows the reconstruction of the segmented parts in the spatial domain. These parts are then merged to obtain the final output image or reconstructed image at the receiver end.
ALGORITHM OF PROPOSED SPIHT METHOD
# Informative part (I) and background part (b) are subjected to transformation
# Wavelet Transform
Step 1: Decomposition levels are given in Eq. (5).
Step 2: Wavelet filter ‘bior 4.4’ is chosen for decomposition into sub-bands (LL, LH, HL, and HH).
Step 3: Decomposition process is repeated until the decomposition level is reached.
# Wavelet coefficients are subjected to the SPIHT encoder.
# SPIHT Encoder
#Different bit rates are selected for foreground (higher bit rate) and background (lower bit rate)
Step 4: It partitions the coefficients into significant and insignificant coefficients using the threshold function given in Eq. (15).
# Sorting pass
Step 5: Using threshold →coefficients are listed into LIS, LIP, and LSP.
Step 6: Maximum bits required by the largest coefficient in its spatial tree representation is given in Eq. (16).
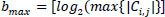 |
(16) |
# Refinement pass
Step 7: Sets present in the LIS will be checked whether they are significant or not.
Step 8: If a particular set is significant →it is divided into subsets.
Step 9: If any subset has only one coefficient and if it is significant→, it will be transferred to LSP, and if insignificant→, it will be transferred to LIP.
Step 10: Terminate the process when the desired bit rate is achieved (till that threshold value keeps on decreasing).
ALGORITHM OF PROPOSED JPEG METHOD
# Informative part (I) and background part (b) are subjected to higher and lower bit rates, respectively, in parallel processing.
Step 1: Input image is divided into small blocks of dimension 8×8.
Step 2: A block of pixels is converted from spatial to the frequency domain using discrete cosine transform (DCT) using the following Eq. (17):
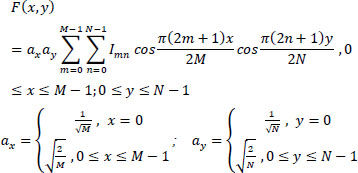 |
(17) |

Block diagram of JPEG compression standard.
Step 3: Quantization of frequency coefficients is performed to achieve a desired compression rate.
Step 4: The grouping of low-frequency coefficients to the top and high-frequency coefficients to the bottom of the matrix by zig-zag scanning of coefficients.
Step 5: Run-length encoding is applied to the coefficients to remove the redundancies present in frequency coefficients.
4.4. Compression Evaluation metrics
The performance of the proposed method is compared with state-of-the-art methods, such as JPEG and SPIHT, using different compression parameters like compression ratio (CR) and peak signal-to-noise ratio (PSNR). The compression ratio of the image is the ratio of the original to the compressed bitstream, and the compression ratio of segmented parts of the image is calculated using the following Eqs. (18-20):
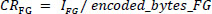 |
(18) |
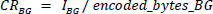 |
(19) |
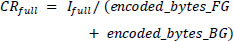 |
(20) |
PSNR is the ratio of peak information value to the power corresponding to noise, and the mathematical expression for PSNR in dB is given in Eq. (21).
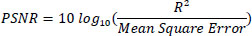 |
(21) |
Where R is the maximum value and different values are assigned to R for different data, and the mean square error is given in Eq. (22) as:
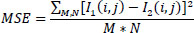 |
(22) |
Where I1 and I2 are input and output images, respectively, and (i, j) are rows and columns, respectively, and M * N is the image size.
Tables 3 and 4 show the mathematical evaluation of PSNR and CR, respectively, for different compression methods tested at different bit rates. In the proposed method, different bit rates are applied to FG and BG parts of the image, whereas other compression standards, like JPEG and SPIHT, process the entire image at bit rates similar to the bit rates of the foreground part of the proposed method. The proposed METEBAC-JPEG and METEBAC-SPIHT methods achieve a higher PSNR of the foreground parts at different bit rates than JPEG and SPIHT, as shown in Table 3. The proposed METEBAC-JPEG and METEBAC-SPIHT methods achieve a higher CR as compared to JPEG and SPIHT. For better visualization of the comparison, a graphical representation of PSNR and CR for different methods is shown in Figs. (5 and 6).
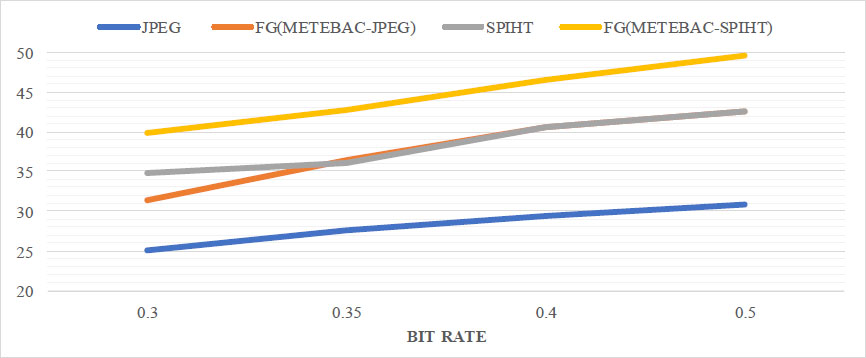
Plot of PSNR for different methods at different bit rates.
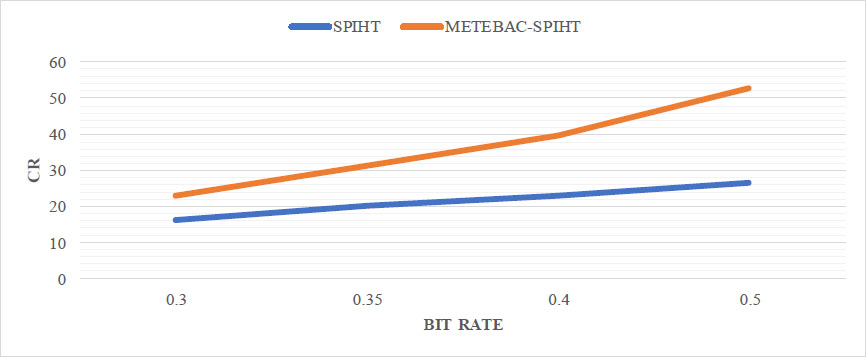
Plot of CR for proposed method v/s SPIHT.
| S.No. | Bit Rates | JPEG | Proposed METEBAC-JPEG | SPIHT | Proposed METEBAC-SPIHT | ||
| - | FG & BG Parts | Full Image | FG Part | Full Image | Full Image | FG Part | Full Image |
| 1. | 0.5 & 0.3 | 30.79 | 42.60 | 31.13 | 42.57 | 49.61 | 39.93 |
| 2. | 0.4 & 0.22 | 29.39 | 40.64 | 29.97 | 40.63 | 46.53 | 41.02 |
| 3. | 0.35 & 0.17 | 27.57 | 36.42 | 28.63 | 36.11 | 42.78 | 36.53 |
| 4. | 0.30 & 0.12 | 24.98 | 31.31 | 26.45 | 34.75 | 39.89 | 34.65 |
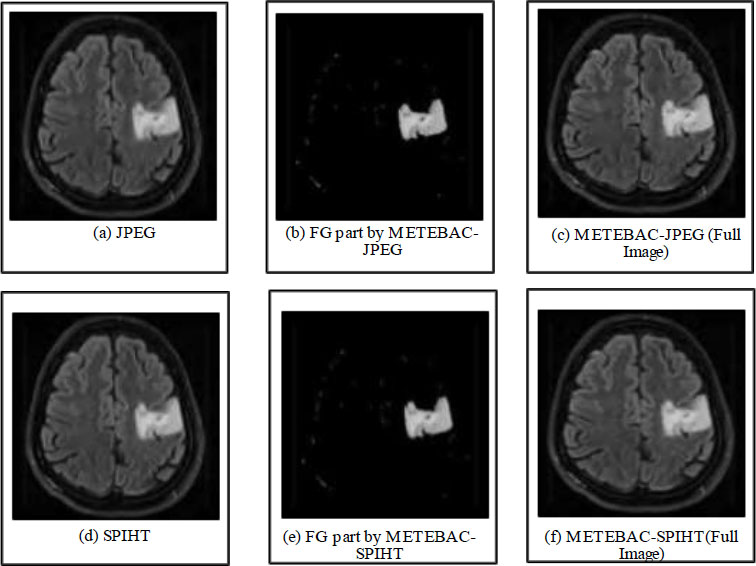
Reconstructed image by a) JPEG, b) Foreground by METEBAC-JPEG, c) Full image by METEBAC-JPEG, d) SPIHT, e) Foreground by METEBAC-SPIHT, and f) Full image by METEBAC-SPIHT at bit rates 0.4(FG) & 0.22(BG)
| S.No. | Bit Rates | SPIHT | Proposed METEBAC-SPIHT | ||
| - | FG & BG | Full Image | FG | BG | Full Image |
| 1. | 0.5 & 0.3 | 16.00 | 16.00 | 26.66 | 22.81 |
| 2. | 0.4 & 0.22 | 20.00 | 20.00 | 36.36 | 31.32 |
| 3. | 0.35 & 0.17 | 22.85 | 22.85 | 45.71 | 39.73 |
| 4. | 0.30 & 0.12 | 26.67 | 26.67 | 66.67 | 52.68 |
It can be observed that the quality of informative parts retrieved back at the receiver end is higher. The empirical evaluation also confirms the effectiveness of the proposed method, such as METEBAC-JPEG outperforms conventional JPEG in terms of PSNR at the same bit rates, and similarly, proposed METEBAC-SPIHT outperforms conventional SPIHT in terms of PSNR at the same bit rates. Overall, the proposed method is able to outperform the conventional compression methods in terms of performance parameters, as illustrated in Table 4. The different reconstructed images from the proposed method and conventional methods are shown in Fig. (7) for qualitative assessment.
Both quantitative and qualitative analyses indicate that the proposed method outperforms different transformation-based compression methods in terms of the visual quality of the informative parts. This improvement can be attributed to the processing of the foreground part at higher bit rates and the background part at lower bit rates.
CONCLUSION
Due to the large size of medical images, especially magnetic resonance imaging (MRI), CT scans need a high bandwidth for transmission and large storage space. Therefore, an effective medical image compression technique is required to attain a high compression rate while preserving the quality of the informative part, which is critical for diagnosis purposes. The proposed method achieved the automated extraction of the informative parts similar to the ground truth images using the proposed segmentation, resulting in an improvement in the compression rate compared to state-of-the-art methods. The mathematical evaluation of the proposed method was carried out using various segmentation and compression parameters. Further, active contour methods could be refined by incorporating image information to avoid leakages through weak edges in noisy images and enabling the accurate extraction of the informative regions, which can result in the improvement of compression rates for the transmission of images.
PRACTICAL IMPLICATIONS AND POTENTIAL CHALLENGES IN REAL-WORLD APPLICATIONS
With advancements in healthcare infrastructure, the production of medical images is rising exponentially, thereby necessitating more storage. Segmentation-based compression techniques play a key role in clinical applications that enable physicians to increase the precision of diagnostic procedures. The precise demarcation of the region of interest is required for effective compression of different medical images to reduce the transmission bandwidth and enhance the storage space. The proposed method provides an alternate notion for the medical staff and produces an efficient compression of different magnetic resonance images while maintaining the quality of the diagnostically relevant information. The therapeutic application of this efficient compression method can be expanded to clinical use for patients in remote locations.
AUTHORS’ CONTRIBUTIONS
The authors confirm their contributions to the paper as follows: L.S.B., S.A., J.S., and A.D.: Study conception and design; L.S.B. and A.D.: Data collection; L.S.B., S.A., and J.S.: Analysis and interpretation of results; L.S.B., S.A., J.S., and A.D.: Draft manuscript. All authors reviewed the results and approved the final version of the manuscript.
LIST OF ABBREVIATIONS
| MR | = Magnetic Resonance |
| FG | = Foreground Part |
| BG | = Background Part |
| RLE | = Run-Length Encoding |
| JPEG-LS | = Joint Photographic Experts Group-Lossless Compression Standard |
| JPEG | = Joint Photographic Experts Group |
| DCT | = Discrete Cosine Transform |
| FCM | = Fuzzy c-means |
| SPIHT | = Set Partitioning in Hierarchical Tree |
| DWT | = Discrete Wavelet Transform |
| CR | = Compression Ratio |
| PSNR | = Peak Signal-to-Noise Ratio |
| CNN | = Cellular Neural Network |
| CV | = Coefficient of Variation |
| SBS | = Saliency-based Segmentation |
| PCA | = Principal Component Analysis |
| MET | = Maximum Entropy Threshold |
| EBAC | = Edge-based Active Contours |
| SPIHT | = Set Partitioning in Hierarchical Tree |
AVAILABILITY OF DATA AND MATERIALS
A total of 50 MRI brain images were taken from the available online database [https://www.kaggle.com/datasets/navoneel/brain-mri-images-for-brain-tumor-detection] for testing the effectiveness of the proposed method [27]. These data were tested in MATLAB R2017b using the proposed algorithm.
ACKNOWLEDGEMENTS
Declared none.


