All published articles of this journal are available on ScienceDirect.
High-Field fMRI for Human Applications: An Overview of Spatial Resolution and Signal Specificity
Abstract
In the last decade, dozens of 7 Tesla scanners have been purchased or installed around the world, while 3 Tesla systems have become a standard. This increased interest in higher field strengths is driven by a demonstrated advantage of high fields for available signal-to-noise ratio (SNR) in the magnetic resonance signal. Functional imaging studies have additional advantages of increases in both the contrast and the spatial specificity of the susceptibility based BOLD signal. One use of this resultant increase in the contrast to noise ratio (CNR) for functional MRI studies at high field is increased image resolution. However, there are many factors to consider in predicting exactly what kind of resolution gains might be made at high fields, and what the opportunity costs might be. The first part of this article discusses both hardware and image quality considerations for higher resolution functional imaging. The second part draws distinctions between image resolution, spatial specificity, and functional specificity of the fMRI signals that can be acquired at high fields, suggesting practical limitations for attainable resolutions of fMRI experiments at a given field, given the current state of the art in imaging techniques. Finally, practical resolution limitations and pulse sequence options for studies in human subjects are considered.
INTRODUCTION
For the sake of this paper, “standard” fMRI resolution is defined as ~3-3.5 mm (isotropic) voxels, or voxel volumes in the range of 20-50 mm3. “High resolution” will be defined as voxels with volumes between 1 mm3 and 20 mm3 (e.g., ~1-2 mm isotropic). The term “ultra-high resolution” will be used to describe functional imaging studies with resolutions better than 1 mm. Regarding field strength, we will use the term “high field” to indicate scanners operating at field strengths of 7 Tesla and above. While 3T is reasonably considered to be a high field strength, it has become the standard field strength for fMRI applications. Therefore, for the sake of simplicity in terminology for this paper, a field strength of 3T will be designated as a standard field strength.
With the ubiquitous implementation of parallel imaging (PI) techniques on scanners at all field strengths, whole-brain high-resolution studies are readily accomplished with temporal resolutions around 3-5 sec. For whole-brain high-resolution studies to achieve temporal resolutions better than 3 sec, advanced techniques [1, 2] are generally required. For ultra-high resolution studies, advanced techniques can also improve temporal resolution (albeit to different levels depending on the spatial resolution and number of slices needed), with SNR and volume coverage being the limiting factors. This overview, however, will not concentrate on issues specifically related to temporal resolution, but will instead focus on spatial resolution in fMRI and issues related to reducing the acquisition times (i.e. volume TR and read-out times) to acceptable levels. The first section on image acquisition and resolution will discuss practical limitations for ultra-high-resolution studies.
One of our central theses is that higher resolution is not always better, i.e., that different neuroscience questions are best addressed at different resolutions. The second section on spatial specificity will discuss the spatial sampling characteristics of different imaging techniques, and match these up against the spatial characteristics of different neural network architectures. Recent advances in both experiment design and in analysis strategies have demonstrated that many questions about neural information processing can be answered at relatively low resolution [3]. Furthermore, even the smallest voxel currently achievable contains tens of thousands of neurons. Because the mechanisms of neurohemodynamic coupling are not fully understood, arbitrarily increasing the image resolution is not always the right approach to understanding the details of the underlying neural code. The second section will discuss signal characteristics for different fMRI techniques, suggesting three different “ideal” spatial scales for neuroscience experiments.
Finally, the third section will consider practical limitations to human fMRI experiments. For ultra-high-resolution studies, the most obvious way to achieve higher SNR is to increase the number of samples (i.e., run several repeats of each scan and average over time). However, human subjects have finite stamina, and even subjects who can remain alert and on-task in the scanner for several hours will exhibit effects of learning or adaptation, making the acquisition of additional data fruitless. Subject motion is another obvious limitation for the effective resolution of a given experiment. In addition, achieving large volume acquisitions studies efficiently at high fields is often not limited by the hardware capabilities, but rather FDA limits on the amount of thermal energy that can be transferred to the subjects head via RF pulses. This last section will discuss such practical limitations imposed on high spatial resolution studies and the recent advances in hardware and pulse sequence design that can mitigate these limitations.
IMAGE RESOLUTION AND IMAGE QUALITY
Gradient Performance
Gradient performance limits the rate at which the large matrices required for high-resolution images can be acquired. A typical Siemens 3T system (i.e. TIM Trio) is equipped with body gradients capable of a 200 T/m/s slew rate and a 40 mT/m maximum gradient amplitude, and a radio frequency (RF) head coil with between 8 and 32 channels. Other vendors such as GE and Philips have similar hardware for their standard 3T systems. Parallel data acquisitions [4, 5] with reduction factors of at least 2 (depending on the RF coil) are reasonable to consider for high-resolution acquisitions to reduce acquisition times. The acceleration or reduction in imaging factor, R, represents the amount of under-sampling in the phase encode direction that is used to acquire an image. The SNR loss imposed by parallel imaging acquisition scales with the square root of R times the g-factor. The g-factor is a noise amplification resulting from an ill-conditioned matrix inverse imposed to unalias the undersampled images. The g-factor depends on R, the number of coils, the coil sensitivity profiles, and the phase encode direction.
Acquiring data with R=2 reduces the echo train length, thereby circumventing limitations imposed by gradient performance and increasing acquisition rates to combat image distortion, signal drop-out, and T2*-blurring (described in more detail below). At 3T, with 2 mm resolutions and a matrix size of 96, the readout time per slice is reduced from ~70 msec to ~35 msec (near the T2* of tissue at 3T [6]). Depending on the choice of echo time (TE) and slice orientation (some orientations incur additional limitations on the rate at which gradients can be switched due to peripheral nerve stimulation), 18-20 high-resolution slices might be acquired per second using a gradient-recalled echo echo-planar imaging (GE-EPI) pulse sequence on this standard 3T system. (Although there are many advantages to employing spiral-based imaging trajectories for fMRI [7], because of the predominance of EPI on both clinical and research systems we will focus this discussion on EPI based methods). With a slice thickness of 2 mm and a pseudotransverse slice prescription, whole-brain coverage might be achieved with a repetition time (TR) of 3 sec. Therefore, 2 mm isotropic voxels with 3 sec temporal resolution is a reasonable reference point for the upper limit of what can be physically achieved (with reasonable SNR, i.e., using a 12 or 32 channel array coil) on a state-of-the-art 3T scanner and standard single shot 2D GE-EPI with parallel imaging (R=2). Other sequence options are discussed further on, however, 2D GE EPI is used here as a reference point because it is by far the most popular choice.
A reasonable expectation for a 7T scanner is that it might be equipped with body gradients comparable to those described for the 3T scanner, and RF head coils with up to 32 channels. However, the shorter T2* values and increased susceptibility artifacts at high field make it paramount to image faster to achieve similar image quality for the same resolutions at 3T. As such, faster, head-only gradient inserts have been designed to further improve image acquisition speeds at 7T. A head-only gradient system, because of its smaller diameter and limited extent in the head/foot direction, can be switched more quickly and achieve higher maximum gradient amplitudes. At the time of writing, Siemens was the only clinical vendor that supported head gradient inserts. The Siemens head gradient insert for 7T is capable of a slew rate of 333 T/m/s and a maximum gradient of 80 mT/m, reducing readout times per slice (for the 2mm resolution with R=2) from ~35msec to ~20 msec (near the T2* of tissue at 7T [8]). With the shorter TE, 30-35 slices can be acquired per second and 2 mm isotropic resolutions over the entire brain are possible in less than 2 secs. Assuming these specifications as a starting point for high-resolution imaging readily achievable at 7T with standard techniques, we will discuss how other hardware and software advances let us take advantage of the increased SNR at high field [9] to acquire images with ultra-high spatial resolution without sacrificing whole brain coverage or temporal resolution.
Parallel Imaging and RF Profiles at High Fields
At high fields, because the RF wavelength nears the size of the object, RF penetration becomes a concern. During transmission, complex phase patterns of different elements generally result in cancellations on the periphery and other (non-superficial) regions, which can result in dark spots in the image, even when maximum flip angles are achieved elsewhere [10]. Further, depending on the specific head, the magnitude and location of these effects can vary, which complicates clinical studies or any study that relies on reproducible methods from subject to subject. However, if multi-channel transmit coils are used (in addition to the multiple receive elements commonly in use), the phase and magnitude of the individual transmit elements can be adjusted (i.e., B1 shimming) to provide an optimized transmit field. The optimized transmit field might entail uniformity throughout the brain, or it might be adjusted to provide maximum efficiency on a target of interest.
On the other hand, on the receive side, because coil sensitivity profiles are used for spatial encoding, the complex receive patterns (which are not detrimental because signal is received from each element separately) can be exploited. As such, a nice synergy exists between parallel imaging and high field, such that g-factors remain low for increased values of R [11], and R=4 in the phase-encode direction (with 16 channel coils) is readily achievable for 7T fMRI applications [12]. Fig. (1) illustrates readily achievable image quality and resolution with standard parallel imaging techniques at 7T. Higher values of R obviously permit significant reduction in the echo train length (total image readout time), albeit at the cost of SNR because of the reduced number of data points acquired and the encoding capabilities (g-factors) of the multi-channel coil. As the next few sections will describe in detail, the loss of SNR is often well justified by the improvement in image quality that results from minimizing the echo train length.
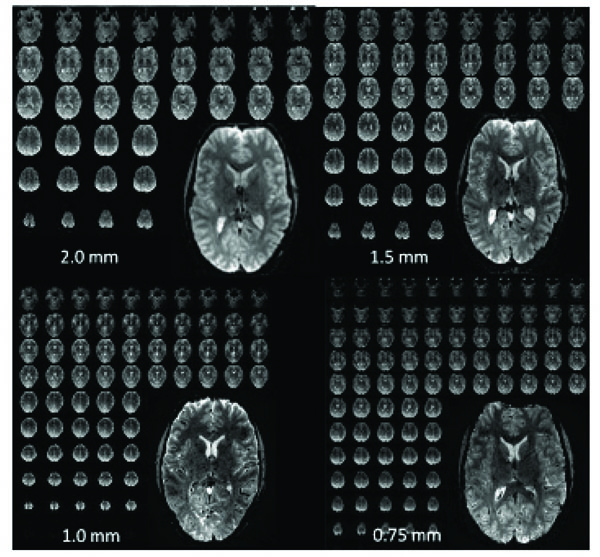
Examples of high-resolution single-shot EPI acquired at 7T over the entire brain with different isotropic resolutions. 2.0 mm: matrix: 96 x 96, 50 slices, TR = 2 s, R=2, readout time: 20 msec. 1.5 mm: matrix: 128 x 128, 60 slices, TR = 3 sec, R = 3, readout time: 21 msec. 1.0 mm: matrix: 192 x 192, 100 slices, TR = 3-4 sec, R=4, readout time: 28 msec. 0.75 mm: matrix: 256 x 256, 128 slices, TR = 4- 5 sec, R=4, readout time: 48 msec.
Ultimately, the reduced read-out trains permitted by increased acceleration factors allow for faster TRs for the same resolutions, depending on the needed TE delay time. TE delay typically is minimized at 7T due to the shorter T2* values relative to 3T. Therefore, increased R values at 7T make large volume high-resolution acquisitions feasible by permitting faster acquisitions for large matrices.
Geometric Distortions and Blurring
Researchers acquiring fMRI data at high field strengths want fast data acquisitions not only to increase spatial coverage and temporal sampling, but also for the added advantage of minimizing image distortions and resolution loss due to long read-out times in EPI. The severity of distortion in EPI images is linearly related to two things: the magnitude of the unwanted field perturbation and the image read-out time [13, 14]. Distortion is therefore more severe at 7T than 3T, for a given image read-out time, because the field perturbations increase with field strength. Likewise, as matrix sizes are increased to achieve higher resolution, the total image read-out time increases. If nothing is done to limit image read-out time, high-field, high-resolution EPI images can have unacceptable levels of distortion.
The increase in readily achievable R-values (i.e.,from R=2 at 3T to R=4 at 7T [1, 12]) approximately offsets the 2.3X increase in severity of field perturbations in the brain, making the move to high field a break-even proposition from the perspective of controlling image distortion (provided sufficient SNR and optimal multi-channel coils are available for a given application). Using fast head-only gradients in combination with parallel imaging further reduces the negative impact of image distortion in EPI images. Fig. (2) shows an example of a 7T GE EPI acquisition at 1 mm isotropic resolution acquired with the body gradients and with the fast head gradient insert. The image distortion difference is considerable as the image read-out time is nearly double with the body gradients. Note, the intent of this figure is only to illustrate what is typically achievable. A full comparison (body vs head gradients) for fMRI optimization would involve many different technical aspects including distortion corrections, differences in bandwidths, and any hardware limits due to duty cycles, acoustic noise, and temporal instabilities.
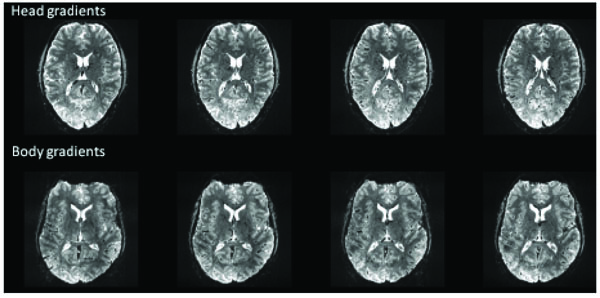
Example (single-shot) EPI images acquired with body gradients and head gradients at 1mm isotropic resolutions at 7T using a 16 channel head coil. Head gradient image parameters: R=4, matrix: 192 x 192, partial Fourier= 6/8, echo spacing=0.58 msec, TE=22 msec, readout time = 18.5 msec (32/48 lines). Body gradient parameters: R=4, matrix: 192 x 192, partial Fourier= 6/8, echo spacing=0.96 msec, TE=25 msec, readout time = 30.7 msec (32/48 lines).
Even the fastest EPI read-out, however, will have some level of geometric distortion. Therefore, every EPI acquisition is typically accompanied by a magnetic field map. Multiple TE (GE) images can be acquired to generate magnetic field maps and then used for post-acquisition correction of geometric distortions [13, 15]. The phase evolution of a given voxel depends on the local field and this local field can be estimated by observing the relative phase at 2 different echo times. The phase difference map can be scaled to represent the measured field inhomogeneity and then converted into a map of one dimensional voxel shifts, which can then be corrected [16-18]. Although not perfect, this technique can significantly reduce geometric distortions in EPI images, and is commonly used in combination with any EPI acquisition strategy (or echo-train reduction), producing high quality functional images.
High-field EPI also suffers from an effective loss in spatial resolution due to the T2* filter effect. The effective blurring or resolution loss of the T2* filter effect is governed by the full width at half-maximum of the Fourier transform of the T2* decay. Keeping read-out times near the T2* of the tissue being imaged results in a minimal loss in spatial resolution [19]. As described above, the use of faster gradients alleviates these problems considerably, which are significantly worse at 7T due to the much shorter T2*s. One should not, however, arbitrarily reduce the echo spacing (or train) when improved gradient performance allows, since this comes at the expense of increased image bandwidth (and therefore reduced SNR). One should choose a compromise between acceptable (correctable) levels of geometric distortion/blurring and larger readout bandwidths. It is also essential, when increasing gradient demands, to consider potential gradient duty cycle limits and/or mechanical resonances which can result in instabilities and/or unacceptable levels of acoustic noise. Such limits will depend on a particular gradient set and image orientation.
Susceptibility-Induced Signal Losses
Another pervasive problem in achieving high-quality fMRI data is the problem of signal drop-out in inferior brain regions due to intra-voxel signal dephasing near air/tissue or air/bone interfaces. This is already a substantial problem in standard fMRI acquisitions at 3T that utilize a 2-3 mm slice thickness, particularly in inferior temporal cortex and inferior frontal cortex; many publications have discussed acquisition strategies to minimize signal loss in these problematic regions [20-23]. Severity of intra-voxel dephasing will only increase at high field as the magnitude of the unwanted field perturbations increases, unless acquisition strategies are modified to combat intra-voxel dephasing.
Fortunately, several aspects of high-resolution high-field acquisitions combat intra-voxel dephasing. As slice resolution is increased (<2mm), images show evidence of decreased susceptibility problems. While dephasing in the through-slice direction is the leading cause of signal loss, increased resolution in the readout and phase encode direction also combats signal loss due to susceptibility effects [16]. Finally, the shorter TEs that are already desirable to match the shorter tissue T2* will also minimize signal loss from intra-voxel dephasing. Therefore, as is the case for image distortions, judicious choices in acquisition strategies can minimize the problems with drop-out, producing superior images at 7T in spite of the additional challenges that come with moving to higher field strength.
Practical Resolution Limits
Fig. (1) demonstrates whole brain (anatomic-like) isotropic resolutions of up to 0.75 mm; voxel volumes are around 64 times smaller than what is done using standard field strengths and resolution (i.e., 3 mm at 3T). These images are presented to give a flavor for what is achievable in terms of the type and amount of data; they are not intended for quantitative comparisons between the different resolutions as the acquisitions are quite different. Such 0.75 mm EPI acquisitions, although conceivable for 7T, definitely push the limits of what is feasible, both in terms of image quality (i.e., SNR and distortions), and in terms of what can be handled by the gradients (duty cycle) and computer hardware (i.e., data acquisition rate). Achieving ultra-high (0.5 mm) in plane resolutions over the whole brain with single-shot EPI and standard methods is currently not feasible, due to the SNR available in our setup (~3.5X smaller voxels compared to 0.75 mm resolution), data rate/size limits, and because of the unacceptably long read-out time. Acceptable image quality (i.e. blurring, distortion, SNR, etc.) for whole-brain, ultra-high-resolution acquisitions (without reduced field of views) would entail further reductions in the echo train length either by improved parallel imaging performance (i.e., larger reduction factors without significant losses in SNR) or by acquiring multiple shots. The multi-shot approach would increase the TR by a factor of 2 or more and increase the contamination from physiological noise due to image segmentation, thereby substantially reducing fMRI efficiency for EPI based techniques. In the foreseeable future, with improvements in parallel data acquisition techniques, we expect our whole brain limit to be around ~0.7 mm isotropic depending on RF/gradient design and CPU capabilities.
For resolutions better than 0.7 mm, very large matrix sizes are needed (e.g., 384 read-out points per line (0.5mm resolution) would require around 0.85ms, even with fast, head-only gradients). Compared to the 1.0 mm and 0.7mm acquisitions, the total full field of view (FOV) (192 mm, anterior- posterior) readout time for single shot 2D EPI, assuming a PE acceleration of 4, would go from ~1 T2* (1.0 mm) and ~ 2T2*s (0.75 mm) to more than 3X the T2* for the 0.5 mm acquisition at 7T using the head gradients. The resulting blurring along the phase encode direction would be more than 50% [19, 24], or an effective resolution which would be larger than the images acquired at 0.75 mm resolution along the phase encode direction. The large matrix sizes make reasonable TEs and acceptable read-out times difficult if not impossible to achieve (not to mention limits in data acquisition rates). As such, some kind of reduction in the imaging FOV, and a corresponding loss of whole-brain coverage, is currently a necessary trade off for such resolutions, unless significant improvements in parallel imaging performance can be achieved, permitting reduction factors higher than 4 with a sufficient amount of SNR retained. Therefore, while whole-brain high-resolution (around 1mm) acquisitions are feasible at 7T with good SNR and acceptable levels of distortion and blurring, ultra-high (0.5mm) resolutions are currently more practical with reduced FOVs and/or volumes. The third section of this paper will discuss several FOV reduction strategies for both gradient echo (GE) and spin echo (SE) acquisitions.
fMRI Sensitivity
A key limitation in acquiring fMRI data with ultra-high resolution is the raw signal-to-noise ratio of the images. SNR decreases linearly with voxel volume, and is proportional to the square root of the number of points acquired (therefore decreasing with parallel imaging). A dominant motivation for working at high field strengths is that the polarization of the proton signal, on which the MRI is based, increases linearly with field strength. This means that the magnitude of the available imaging signal at 7T is ~2 times greater than at 3T [9], providing obvious advantages for high-resolution imaging.
Of course, for an fMRI experiment it is the contrast-to-noise ratio (CNR) that determines sensitivity. CNR depends on the image SNR, the magnitude of the BOLD contrast, and the temporal noise. Fortunately for high-resolution, high-field applications, BOLD functional contrast (i.e., susceptibility effects) increases rapidly with field strength. Further, the tissue response experiences a supra-linear increase with field strength [8, 25], while the large vessel component increases only linearly, making the BOLD contrast at high fields not only much higher than low fields, but also potentially much more specific.
While both image SNR and contrast are greater at high field, the temporal signal to noise ratio (tSNR) must be considered to determine the ultimate sensitivity (CNR) of an experiment. This depends on both the static image SNR and the physiological noise [26-30]. While BOLD effects are much stronger at 7T than at 3T, physiological noise is also amplified (relative to thermal noise) at high fields, particularly with low spatial resolutions [27, 31]. As such, it has been suggested that 7T (and higher) fMRI applications may not realize significant differences in fMRI sensitivity over 3T and lower fields [26, 32]. However, the potential sensitivity advantages of high field depends on the image resolution: small voxel volumes will put an experiment into the thermal noise-limited regime at 3T but taking the experiment to high field will increase image SNR and move the experiment into the physiological noise-limited regime, where the net CNR is better. One estimate of the theoretically optimal image resolution at 3T, balancing thermal and physiological noise, is 1.8 mm (isotropic) voxels [32]. Of course, the exact number will depend on coil sensitivity. But using this as a rule of thumb, it is reasonable to expect that fMRI experiments with resolution of 1.5 mm or higher will be thermal-noise limited at 3T and will benefit significantly from the increased SNR and fMRI contrast at 7T.
For 7T acquisitions, the thermal noise limit may permit isotropic resolutions of around 0.5-0.75 mm. However, surpassing the thermal noise limit over the entire brain, due to inefficient RF volume coil design, may not yet be feasible at these resolutions. As such, currently ~1mm acquisitions over the entire brain (for GE acquisitions) may be a more realistic achievement, with localized applications/areas (i.e., visual areas or surface coils) permitting higher resolutions.
SPATIAL SPECIFICITY OF FUNCTIONAL MRI SIGNALS
Simply acquiring images with small voxels is not sufficient to ensure high-resolution measurements of neural responses. Since the fMRI signal samples a vascular response; its resolution depends on vascular geometry, hemodynamic regulation, and neuro-hemodynamic coupling. This section provides a brief summary of what is known of the vascular signal source for different fMRI modalities, as well as a brief summary of neural architecture that suggests different optimal scales for measuring different neural responses.
BOLD Specificity
The BOLD signal [33-36] measures the hemodynamic response to neural activity by exploiting the magnetic properties of blood water. BOLD fMRI is sensitive to any changes in CMRO2, CBF or CBV, all of which alter the relative amount of deoxyhemoglobin, and thus the local magnetic field in the brain. Despite this indirect nature of the BOLD mapping signal, it has been shown to be well correlated with the underlying neuronal activity [37, 38]. GE and SE BOLD fMRI at low fields are subject to a dominating intravascular blood effect that is strong even at long echo times because of the long blood T2 [39-42]. As the intravascular effect is diminished because of the shortening blood T2 at high fields, the extravascular effect becomes dominant, and, ultimately, we are left with a BOLD signal that reflects extravascular effects around large and small vessels for GE and more significantly around small vessels for SE, since large vessel effects are refocused in SE-based fMRI [25, 41, 42]. A more complete modeling of the signal characteristics of the BOLD signal was recently published and quantifies these effects in detail [43].
Experimental Measurements of the BOLD Specificity
Several estimates of the spatial accuracy of fMRI data based on GE EPI characterize the signal with a Gaussian blurring kernel with a full-width at half-maximum (FWHM) of 3-4 mm [44-46]. However, it is important to remember that striking heterogeneity is found in the population of voxels acquired in a GE fMRI experiment [47, 48]. Kriegeskorte et al. (2010) discusses the pitfalls of modeling all voxels with the same Gaussian kernel, pointing out the added complication that the spatial sampling of the fMRI response changes through time due to transit times in different venous compartments. Therefore, while 3-4 mm is a reasonable rule of thumb for GE spatial accuracy, some voxels show evidence of displacing signal by more than 5 mm [49], and some GE fMRI voxels have demonstrated spatial precision better than 1 mm [50-54]. Some of this variance may be explained by the different field strengths used for these studies, but some of this variance is a necessary consequence of the vascular geometry and the relative locations of different voxels with respect to large veins. Therefore, unless large vessel effects are explicitly accounted for, suppressed, and/or avoided, which is not straightforward in human studies, the mapping signal of GE BOLD can be significantly degraded [46, 55].
The variability of the GE BOLD spatial specificity is never more evident than in Fig. (3) (taken from [56]), which shows an example of ODC mapping in humans at 7T using GE and SE based BOLD signals. In this case, where even differential mapping was used to map the columns, residual effects from large veins (outside of the slice) persisted in some parts of the imaged slice, precluding the resolution of the columns. However, in other parts of the slice, where the tissue areas are more distant from large vessel effects, the columnar organization is retained. These data demonstrate the heterogeneity of the GE BOLD point spread function versus the much more homogenous SE BOLD signal.
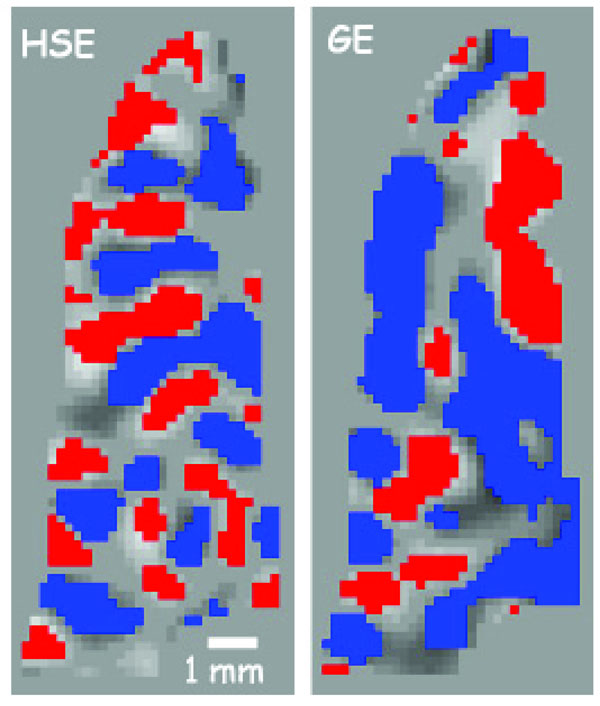
ODC maps from a flat gray matter region along the calcarine sulcus from the same subject on several different days. On the left is the overlap of 2 different scan days using SE at 7T, while on the right is the overlap of 2 different scans using GE. Red or blue pixels indicate a voxel’s preference to right or left eye stimulation. The expected spatial pattern is an alternating preference (1 mm width, 2 mm cycle) to right or left eye running along the sulcus. The SE map retains this pattern throughout the region, while the GE map is interrupted by extravascular changes around large vessels somewhere near the region of interest. (taken from Fig. (5) in Yacoub et al 2007 [56] ).
Alternatives to BOLD Based fMRI
As seen in Fig. (3), a well-known limitation of the spatial specificity of the BOLD signal is its dependence on signal changes arising from deoxyhemoglobin concentration around veins, which are downstream from neuronal activity. Alternatives to the GE BOLD technique, such as arterial spin labeling (ASL) [57, 58], cerebral blood volume (CBV) measurements [59, 60], or SE BOLD at high fields, could in principle be used to improve the spatial specificity of fMRI by exploiting contrast from the arterial supply or capillary bed.
The most popular alternative to GE BOLD, ASL, is based on the fact that the magnetization and relaxation characteristics of tissue water are affected by the inflow of blood water. ASL therefore benefits from the increased T1 of blood water at higher magnetic fields: tissue specificity of ASL improves because of the fact that tagged spins require a finite amount of time to reach the capillaries and exchange with tissue water. An MRI study conducted using measurements of CBF directly [61] has demonstrated that CBF changes can be specific at columnar resolution provided that compulsory and accompanying blood flow increases in large vessels feeding and draining the activated region are not simultaneously detected. This was confirmed by an optical imaging study [62] using CBV measurements as a reflection of CBF; the optical imaging study further demonstrated that maps relying on such CBV changes, and presumably CBF changes, can be as specific as those obtained by means of the initial dip [63-65] provided that large surface vessel-signals are nulled.
In spite of advancements in methods for high-resolution arterial spin tagging in humans [66], mapping of sub-millimeter structures in the human brain using this technique has not yet been demonstrated due to SNR limitations, even at high magnetic fields. Non-invasive MR methods to obtain CBV-weighted contrast for fMRI studies, such as VASO [60], have also demonstrated promise as an alternative to GE BOLD to improve the spatial specificity of fMRI. However, like CBF, CBV techniques suffer from insufficient SNR, when millimeter or sub-millimeter spatial resolutions are desired. The use of contrast agents to obtain CBV-weighted fMRI images in animals provides gains in both functional contrast and spatial specificity over BOLD [50, 51, 67-69], however, the application of such techniques to humans remains uncertain because of dosage requirements and the feasibility of doing follow-up studies. As such, the BOLD response (GE or SE) is currently the only viable option for human fMRI studies looking to capitalize on the intrinsic gains in spatial resolution achieved at high fields, with the aim to investigate high resolution functional architectures or organizations.
What fMRI Resolution is Desirable?
One question worth asking is: what is the ideal spatial resolution for a neuroscience experiment? Here, we will make the case that there is not just one answer to that question, arguing for three spatial scales: standard resolution (3-5 mm), to study different neural responses in different cortical areas; high resolution (1-2 mm), to study the spatial characteristics of the neural response within and across different cortical areas; ultra-high resolution (<1 mm), to study the different neural tuning properties that make up the neural population code.
From the perspective of the neural architecture, there are at least three different scales at which neural response properties are organized: the column, the hypercolumn, and the cortical area. At the finest spatial resolution, neurons with similar response properties are clustered in cortical columns, which span the cortical depth with a diameter in the range of 0.2-0.5 mm [70]. A hypercolumn in primary visual cortex (V1) is a reasonable example of the intermediate spatial scale of the neural population code – a region of cortex approximately 1 mm x 1 mm that contains a complete set of columns representing different visual stimulus attributes. Finally, the segregation of cortical areas (defined as regions of neocortex containing neurons specialized to represent information relevant for one particular aspect of behavior) establishes a large-scale neural structure, with each cortical area spanning several centimeters across the cortical surface.
fMRI with standard resolution (and field strength) may be appropriate for experiments that simply ask the question “Does this cortical area encode this kind of information?” or “For what type of task does this region of the brain show specialization?” With the increased sophistication of multi-voxel pattern analysis (MVPA) [3, 71, 72], many groups have demonstrated that low-resolution fMRI data can reveal details about the information encoded by different neural responses in a given cortical area, even though the structure of the underlying neural architecture has a characteristic spatial scale an order of magnitude finer than the fMRI resolution. Therefore, investigators interested in understanding what type of information is represented by neural populations in a given cortical area may not be motivated to seek out high field systems and confront technical issues, or incur any penalties in volume coverage, TR, or SNR resulting from acquiring high resolution images.
Some neuroscience questions, however, need to distinguish neural populations that encode different kinds of information but are located close to each other (e.g., within the same cortical area, separated by less than a centimeter). A low-resolution decoding experiment, which cannot separately quantify the two neighboring population responses, can detect that the information represented in the cortical area is different between two stimuli or behavioral conditions. However, experiments that want to go beyond detecting the differences and to start understanding the mechanisms by which closely juxtaposed neural populations encode different stimuli or behavioral events, require higher than standard resolutions. Many of these experiments do not require columnar resolution, but can be accomplished with ~1 mm resolution. An example might be an experiment investigating the mechanisms by which neural populations representing neighboring visual features in primary visual cortex affect each other – hypercolumn responses need not be resolved, but clusters of hypercolumns separated by 2-3 mm must be clearly distinguished and GE BOLD fails to do so [73]. Similar experimental questions might be: the coarse organization of object representations in lateral occipital complex, spatiotopic organization of parietal cortex, or potential somatotopic organization of supplemental motor area. These represent a family of neuroscience questions that require high resolution to distinguish heterogeneous neural responses within a cortical area, but which do not merit the SNR and FOV challenges that accompany ultra-high image resolution. These experiments stand to benefit greatly from the increased SNR at high field [74], as well as potential increases in temporal resolution.
Finally, the structure of columns and hypercolumns can only be resolved with ultra-high resolution fMRI. Therefore, experiments aimed at understanding the details of the underlying neural architecture itself require sub-millimeter resolution along with high spatial specificity. As discussed above, this kind of functional resolution, although achieved with GE methods, is most reliably achieved in humans with SE-based fMRI techniques (Fig. 3), albeit with reduced volume coverage and SNR compared to GE techniques [56, 75]. The third section of this paper will discuss current pulse sequence and hardware options for achieving ultra-high resolution functional images.
Spatial Specificity vs. Functional Specificity
A separate question from spatial specificity is functional specificity, or the ability to infer accurately local changes in neuronal activity from localized changes in the fMRI signal. All imaging modalities sample the neural population response on a scale that combines the responses from thousands of neurons, some of which are excitatory and some of which are inhibitory, some of which receive inputs from neighboring neurons and some of which receive synaptic input from neurons in different cortical areas. Many neuroscience questions require the ability to detect these different kinds of neural activity within the local (hypercolumn) neural population, which provides a significant challenge for any imaging modality: even single-unit recordings exhibit a bias in sampling the neural population [76], preferentially recording from large excitatory neurons and often failing to characterize the responses of small inhibitory neurons that are nonetheless crucial to forming the local population code.
In the following paragraphs, we will describe two examples of the technical challenges that modern neuroscience experiments face in developing working models of the local neural population code that characterize the information content with sufficient detail to teach us about how the brain accomplishes particular calculations. With both electrophysiology and standard fMRI techniques, we can measure the type of information that is represented in a given brain area. The next step is to understand how the local neural population code computes behaviorally relevant information and adapts these computations to changing environmental demands.
A classic example of the difficulty of achieving functional specificity is the challenge of distinguishing between facilitation and dis-inhibition when studying contextual modulation of neural responses in primary visual cortex (V1) [77]. Behaviorally, the calculation of local orientation contrast is important for detecting texture boundaries. At the individual neuron level, the firing rate of a V1 neuron tuned to image structure at a particular orientation is almost always inhibited when a preferred stimulus in its receptive field is flanked by a parallel stimulus. When the preferred stimulus is flanked by an orthogonal stimulus, however, the firing rates of the target neuron can increase over the strength of a baseline response to the preferred stimulus alone. Two different mechanisms could result in the increased firing rate in the presence of an orthogonal flanker. On the one hand, the increased response to orientation contrast could be the result of a release from inhibition: the target neuron could be subject to low levels of (iso-orientation) inhibition when its preferred stimulus is presented in isolation (because neighboring neurons with partially overlapping receptive fields are stimulated and provide iso-orientation inhibition to the target neuron). Presenting the orthogonal flanking stimulus may result in cross-orientation inhibition of the neighboring neurons (whose receptive fields contain parts of both the target stimulus and the orthogonal flanker), decreasing the strength of the (baseline) inhibition from neighboring neurons with overlapping receptive fields. On the other hand, the target neuron could simply receive facilitation from neighboring neurons that respond to the orthogonal flanking stimulus. Understanding the difference between facilitation and disinhibition is important for understanding how information is combined in the local neural network. However, even with electrophysiology (or ultra-high-resolution fMRI (i.e., Fig. 3)), multiple experiments are required to achieve functional specificity and disentangle the separate contributions of local excitatory and inhibitory connections to fully characterize local neural computations.
The challenge of obtaining functional specificity – the accurate interpretation of an increase or decrease in local signal – is even greater for fMRI data acquired at standard- or high-resolution. When spatial specificity (and resolution) is on the order of 2 mm or more, heterogeneous responses in closely juxtaposed neural populations can be confounded, which further degrades functional specificity. As an example we will consider the results of different fMRI experiments attempting to quantify iso-orientation inhibition. For large stimuli that create neural population responses that are homogeneous across large portions of the cortex [78-80], the results of electrophysiology and fMRI experiments measuring contrast response and orientation-dependent surround suppression are identical. However, for smaller stimuli (which result in neural population responses that are heterogeneous on a scale comparable to the sampling resolution of GE fMRI) hemodynamic and electrophysiology results do not agree [73, 81]. Because both fMRI and electrophysiology are subject to sampling bias and limitations in functional specificity, the disagreement in these results does not mean one methodology or the other is in error. In the particular case of the study by Schumacher and Olman (2010), in which the BOLD response failed to show suppression known to be present in the neural responses, the apparent discrepancy can be reconciled by accounting for (1) the fact that electrophysiology samples only neurons tuned to the orientation of the suppressed stimulus, while high-resolution fMRI samples the average neural population response, which includes neurons tuned to flanking orientations that are released from local (unturned) suppression when the target population is suppressed (i.e., the average response in the hypercolumn is not suppressed by small surround stimuli, even though the column tuned to the target orientation is), and (2) the relative balance of long-range/tuned and local/untuned suppression depends on the size of the stimulus. The disagreement demonstrates that as we push toward a more detailed understanding of local neural activity, we will need to develop more sophisticated models of the local population response and to design experiments that sufficiently constrain our interpretation of underlying neural mechanisms. The evolution of higher spatial resolution and specificity of functional imaging will further disentangle these differences.
One recent advance in fMRI techniques is the ability to distinguish fMRI responses at different cortical depths [50, 82-85]. This capability has the exciting potential to improve our understanding of local neural computation. Neurons with different input/output characteristics are reliably located at different cortical depths [86]. An increase in the neural response in Layer 4 therefore indicates a different mechanism for the modulation of neural activity than an increase in the neural response in Layers 2/3. The total cortical thickness is generally found to be between 1.5 and 4.5 mm [87], while the 6 cortical layers are not all the same thickness, with 2/3, 4, and 5/6 representing the major divisions. Each occupies approximately a third of the cortical thickness in sensory areas, while 5/6 is much thicker in motor areas. Standard and high-resolution fMRI confound these signals, but ultra-high resolution fMRI may be able to distinguish neural activity at different layers (albeit with potential surface contamination effects) and would represent a great advance in the functional specificity of the fMRI signal. Fig. (4) shows an example of ultra-high-resolution fMRI data (0.7 mm isotropic, using a single shot T2 weighted 3D GRASE sequence (discussed further on) with reduced FOVs [88-91]). The functional map depicts robust activation in response to the presentation of partially occluded objects; a sparse distribution of clusters of active voxels is expected and observed in response to these isolated image features. This ultra-high resolution permits separate analyses of these fMRI responses in superficial and deep V1 gray matter [89]. However, whether the spatial specificity is sufficient to resolve layer specific effects is unclear. Previous layer-specific fMRI studies have shown a dependence of BOLD signal changes on cortical depth- not layer specific modulations due to changes in neural processes. The sensitivity of fMRI to such changes would enable experiments investigating how global image organization affects the perception and neural representation of individual image features.
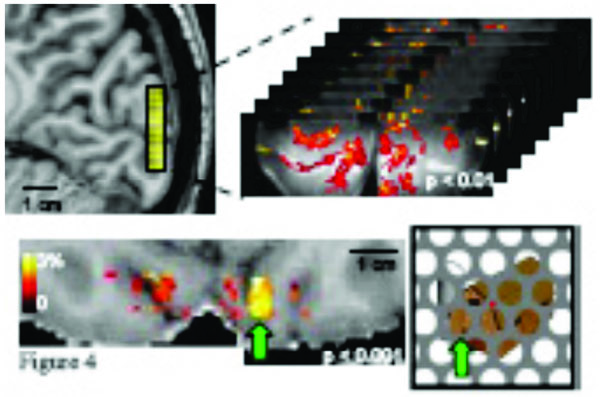
Top panel: a 3D GRASE coronal slab with 0.7mm (isotropic) resolution and 8 slices covers 0.56 cm in the anterior/posterior direction and shows robust activation in response to the presentation of partially occluded objects. Bottom panel: functional responses are visualized as a color overlay on an axial view of the subject’s T1-weighted anatomy (also with 0.7mm resolution). Example stimulus shown at right; green arrow indicates correspondence between a specific cluster of activated voxels and the corresponding image region.
CONSIDERATIONS FOR HUMAN FMRI
With the goal of being practical in this discussion of what is possible using high-field fMRI, this section discusses the issues that arise in fMRI experiments using human subjects that limit the achievable resolution for a given experiment. These practical issues are the ones that make it difficult to predict the true resolution of an experiment without actually trying it (e.g,. one subject may move more than another). Piloting a study on a subject with good stamina will suggest higher achievable resolution than is generally practical given that less ‘good’ data can be acquired with subjects who are less comfortable or more motion prone in the magnet. As exclusive enrollment of good subjects is not always feasible, mitigating these limitations with improved hardware, increased sensitivity, or pulse sequences which optimize data acquisition rates and minimize SAR is paramount. Therefore, the bulk of this section discusses these technical advances that continuously improve the resolution, sensitivity and practicality of fMRI experiments.
Motion
Awake, behaving human subjects cannot hold perfectly still, and when image resolution is less than 1 mm, subject motion is guaranteed to be a concern even for the best subjects. Many high-resolution studies use a bite bar to provide a reliable point of reference for good subjects who want to hold still. However, although bite bars restrict motion, they do not eliminate motion. Many excellent motion compensation algorithms [92] can compensate for motion in the post-processing so that blurring due to motion is comparable to the scale of the imaging voxel. However, many motion compensation algorithms perform poorly on data with a limited field of view, and manual intervention is required to achieve desirable results. Furthermore, the design of an ultra-high resolution experiment must also anticipate the loss of data from peripheral slices, due to subject motion. As such, for ultra-high resolution imaging it is imperative to restrict and monitor motion during an experiment and/or use ideal subjects, along with smart post-processing motion compensation. Continued expansion of volume coverage of high and ultra-high resolution fMRI images (i.e., Fig. 1) will be most effective at mitigating issues of motion compensation by facilitating the success of correction algorithms.
SAR
Limitations due to SAR (specific absorption rate, or the rate at which the pulse sequence transfers thermal energy to the subject’s head) are an often discussed problem of high-field imaging. Because higher energy RF pulses must be used at high fields, experiments run up against SAR limits much more quickly than at 3T. While SAR limits are rarely reached for GE fMRI experiments, SE fMRI – which is a natural choice for high-field applications because of the increased spatial specificity and quadratic increase in CNR with field strength [25] – uses additional RF pulses that can result in limitations in data acquisition rates. As a general rule, if a conventional whole-brain coil is used for a standard 2D-SE EPI acquisition, SAR limits data acquisition rates to approximately 12 slices/second. Further, since fat suppression pulses are typically needed in SE EPI imaging, the SAR restrictions can be even more limiting.
There are, however, several options for mitigating issues with SAR in SE fMRI experiments at high field. First, one can use a surface coil, or an array coil that covers a limited portion of the brain. The next sub-section discusses some details of RF coils for high-field experiments. Alternatively, one can use B1-shimming to improve the efficiency of an SE fMRI experiment by controlling the spatial pattern of thermal energy deposition to optimize acquisition in a specific region of interest or to remove “hot spots” where excess B1 is applied [10, 93, 94]. Finally, on-going pulse sequence development is exploring alternatives to the standard Hahn spin echo approach [95] in order to acquire T2-weighted images while minimizing the power used by the pulse sequence. For example, 3D GRASE [88], SIR EPI [96], and SPIF [97] all achieve T2 weighting (efficiently) with reduced SAR compared to 2D-SE EPI, albeit with some tradeoffs in distortions, slice resolution and/or pure T2 weighting. Options for T2 weighted fMRI are discussed in detail further on.
Coil Design
Many factors affect the choice of RF head coil for an experiment, and in turn, the RF coil determines the achievable SNR of that experiment. At standard field strengths, head coils tend to be receive-only designs, whereas at 7T, body transmit RF coils are not typically used and thus localized transmit and receive head coil designs are needed. Although such RF transmit approaches, along with multi-channel transmit, can be optimal for 7T applications, they can be problematic for fMRI experiments where a sufficient amount of space is needed for visual presentation. More and more whole-brain coils are being designed for 7T that permit the subject to see out of the coil, keeping elements away from the eyes, while not impinging on the ability to achieve whole-brain coverage. However, the subject’s visual field of view can still be limiting. To make RF coil design even more challenging, if the high performing (desirable) head gradients are used, the space inside the bore decreases to around 36 cm. As such, for visual fMRI studies, open (half volume) design surface coils (or arrays) are often used, especially for ultra-high resolution studies of visual cortex.
More obvious factors in coil selection and experiment design are related to sensitivity, power requirements, parallel imaging performance, and uniformity of coverage. The first section discussed the fact that raw image SNR is a strong motivation for moving high-resolution experiments to high field. Using a surface coil for data acquisition, or a local array of surface coils, is also a common way of increasing SNR for ultra-high resolution experiments. Obviously, this is an option only for applications in which the cortical region of interest is readily accessible using a surface coil – generally, primary sensory and motor areas. Also, surface coils are only practical when extended volume coverage is not a concern (for ultra-high-resolution studies, whole brain and/or large volume or whole brain acquisitions are typically not feasible in any case). The non-uniform sensitivity profiles of surface coils presents a challenge for applications requiring uniform contrast between gray and white matter, but it has recently been shown that if a T1-weighted volume is normalized by a simultaneously acquired proton density-weighted volume [98], cortical surface segmentation is possible even on partial-brain anatomies acquired with surface coils [99]. Finally, surface coils with an open design are also much more accommodating to the use of bite bars to restrict subject motion, which can be critical to the success of sub-millimeter fMRI applications [56, 75].
Ultimately, because the design of the RF coil determines not only sensitivity and volume coverage but also efficiency of parallel imaging, the actual SNR of a given experiment is strongly hardware-dependent and difficult to predict in general terms. In addition, since there are many factors in determining the ideal RF coil from an fMRI paradigm perspective, application-specific decisions are typically made with respect to the choice of an RF coil. Clearly, where large volume coverage is warranted, whole brain coils are needed, while a need for accessibility to the subject requires more open coil designs which can be optimized for the cortical region of interest, at the expense of volume coverage. However, as RF coil technology and design continue to evolve, it is conceivable that a single design may eventually be optimal for a vast majority of fMRI studies.
Pulse Sequence Design
As mentioned in the first section of this paper, the overwhelming majority of human fMRI studies rely on the susceptibility-based BOLD effect, mainly because of its high contrast to noise ratio. However, to achieve BOLD contrast, there are of plethora of MR pulse sequences that have been proposed. The choice of pulse sequence is weighted strongly by the demands of the neuroscience question being asked. For example, while a better understanding of the hemodynamic response function (i.e., event related fMRI) warrants sequences which permit high temporal resolutions, the understanding of functional organizations requires high spatial resolution. Further, it is challenging to acquire high spatial resolution data with high (or even acceptable) temporal resolution, and because of the reduced power of event-related designs they become difficult to execute at high resolution. Applications such as resting state fMRI would ideally want high spatial and temporal resolution, as well as large volume or whole brain coverage. Such a capability [1, 2], is currently being pursued as part of the Human Connectome Project by the National Institutes of Health (NIH) (http://www.humanconnectome.org/consortia/). Finally, to make things even more complicated, the spatial specificity requirements of the neuroscience question (i.e., 2-3 mm vs. 1mm or less) are also highly relevant when choosing a pulse sequence, since there are tradeoffs between achievable contrast to noise ratios and spatial specificity.
Non-EPI Based Approaches
To date, nearly all fMRI studies at both low and high fields utilize 2D or 3D single (or multi) shot EPI [100, 101] or spiral based acquisitions [102-105] due to the efficiency of the sequence, which is paramount for fMRI studies. For example, FLASH imaging [106], which has been successfully implemented, requires extremely long acquisition times (30 sec – 1min) and is not practical for most human fMRI studies [84, 107, 108]. Radial methods [109], which are less sensitive to physiological noise and motion, over sample the center of k-space, particularly k0, making it less efficient in terms of k-space coverage per sequence time. Cases can be made to utilize non-EPI based acquisitions for some applications which require reduced distortions, motion artifacts, or susceptibility effects, however, the vast majority of fMRI studies cannot afford the penalty in efficiency, especially since there are numerous ways to mitigate artifacts in EPI. Spiral sampling trajectories have been shown to have advantages over EPI for fMRI [7] with the associated artifacts manifesting as blurring. In spiral imaging, the center of k-space is sampled first and frequency differences due to magnetic field inhomogeneities result in signal propagation during the readout and ultimately image blurring. Improved performance over EPI for fMRI has been observed for spiral sequences and is attributed to lower sensitivity to physiological noise or motion. Spiral imaging is, however, more sensitive to gradient imperfections or errors. The increased technical requirements of spiral have slowed its progression into clinical scanners and as such the vast majority of investigators use EPI. We have chosen here to focus this review on EPI based techniques, but it should be noted that spiral imaging could ultimately be used with some advantages and different limitations then EPI.
2D vs. 3D Sequences
Most fMRI studies typically employ single-shot 2D EPI acquisitions because the acquisition time for a single slice as well as for an entire volume is extremely fast (on the order of tens of msecs for a slice and 2-3 sec for a volume). Single shot or segmented 3D (i.e. echo volume, EVI [101], gradient and spin echo, GRASE [91]) sequences have the advantage of higher SNR (due to the 3D FFT), however, the acquisition time for a given slice is convolved over the volume acquisition time, making the acquisition potentially sensitive to motion and physiological noise. This is similar to the long slice TRs and resulting physiological noise present in segmented 2D EPI acquisitions. Longer volume acquisition times are typically required since 3D acquisitions are usually segmented to prevent long readouts of any single excitation and sampling period. Long readouts can result in distortions and blurring, which are now present on 2 of the image axes, as well as SNR losses. Historically, this has resulted in the use of 2D techniques for most applications, and 3D approaches when a large isotropic volume is required, when temporal resolution is not critical, or when SNR is limiting in 2D acquisitions.
However, 3D acquisitions, like 2D, can capitalize on accelerated acquisitions using phase encode reductions. Further, since 3D utilizes 2 phase encode directions, accelerations along two dimensions can be achieved, reducing even more the acquisition times, allowing for much more efficient 3D acquisitions. Poser et al., [110] showed that with the ability to accelerate along the slice direction, the 3D acquisition time was reduced to levels faster than what can be achieved with 2D imaging, resulting in an overall improved performance of 3D functional images over 2D. This study, however, did not utilize recently implemented slice-acceleration techniques. Multi-banded EPI for 2D acquisitions, allows up to a 4-fold faster volume TR without losses from data undersampling [1], as is present in 2D accelerations of 3D acquisitions. Simultaneous echo refocusing (SER) [96] can also reduce significantly the 2D multi-slice volume TR without SNR losses. Further, the combination of these techniques can provide additional reductions in the volume TR, resulting in large gains for fMRI [2]. 2D Multiplexed EPI [2] allowed for whole brain fMRI acquisitions of around 6 times faster than conventional methods, albeit it was demonstrated with 2-3mm acquisitions at 3T. With this sequence, whole-brain coverage with a temporal resolution of around 1 sec (depending on PI performance) and a spatial resolution of around 1-1.5 mm is a reasonable expectation at 7T. 3D PRESTO SENSE [111-114] (a multi-shot 3D EPI technique) has also been proposed to reduce the acquisition using the TE contrast preparation time between the RF pulse and the next readout period to apply the subsequent excitation pulse, and then separating the readouts by echo shifting. The usefulness of this method depends on the needed TE and at 7 T, due to the shorter TEs used, there may not be enough time to acquire shifted echoes from the prior excitation, especially if high resolutions are desired [115]. Also, there is an SNR penalty in PRESTO and 3D sequences in general because the faster excitation TRs require the use of smaller flip angles [111, 114, 116].
Ultimately, the choice between 3D and 2D acquisitions can be determined by whether or not physiological noise (or acquisition time) will limit the functional sensitivity of 3D acquisitions and whether or not 2D acquisitions have sufficient static SNR. Further, for ultra-high resolution applications, the use of isotropic resolutions requires ultra-thin slices (see application of 3D GRASE in Fig. 4), which can be problematic for 2D acquisitions because of slice profile issues in addition to the low SNR of the high resolution images. To date, although there are more and more papers establishing the superiority of 3D techniques for many applications, continued improvement in efficiency and quality of 2D techniques (resulting from advances in MR technology such as gradient performance, RF coils, pulse sequence design, etc.) have allowed 2D techniques to remain highly attractive to neuroscientists.
T2-Weighted Pulse Sequences
At high fields, because ultra-high resolution neuroscience questions can and are being asked, the presence of highly spatially specific BOLD signals becomes a concern when deciding on a pulse sequence. So, at the expense of reduced contrast to noise, T2-weighted approaches can and have been employed to address these questions [56, 75], albeit with a different set of limitations compared to GE acquisitions. First, fast or extremely fast TRs are not typically employed, due to the insufficient SNR and CNR. The low SNR is likely the result of inhomogeneous RF fields, which reduce flip angles and subsequent image SNR. This problem is significantly magnified in SE images over GE images because of the need for a 180 degree refocusing pulse in SE acquisitions. Further, at 7T (where SE acquisitions are typically employed because of increased sensitivity and specificity of BOLD images), faster or even efficient acquisitions are difficult to achieve because of SAR.
Given all of these practical constraints for the implementation of T2-weighted or SE BOLD techniques, the sequence options are more limited. Although sequences such as: SSFP [117], HASTE [118, 119] (or TSE/FSE) have all been proposed for T2-weighted BOLD, none of them have achieved the necessary combination of efficiency, spatial resolution, functional contrast and specificity to be viable for ultra-high resolution applications, which are the main reason for using T2-weighted BOLD in the first place. To date, only 2D SE-EPI has demonstrated a neuroscience utility as well as an advantage over conventional GE-EPI. In this application (Fig. 3), albeit using a reduced FOV approach which was necessary to achieve efficient high-resolution T2-weighted images, 2D SE-EPI was shown to be a better alternative than GE EPI, allowing the uninterrupted mapping of ocular dominance [56] and orientation columns [75] in humans. Under development are single shot 3D variations of reduced FOV 2D-EPI (i.e., single shot 3D GRASE with inner-volume excitation (Fig. 4) [89, 90]), which provide a means to efficiently extend the volume coverage of 2D SE-EPI, while maintaining functional specificity (discussed further on).
Reduced FOV Approaches
Using a (2D or 3D) reduced FOV approach is extremely advantageous to achieve ultra-high spatial resolutions (i.e., 0.5 mm in plane) efficiently and without resolution or image quality losses due to the required longer read-out trains. Thus, this approach has been the method of choice for 2D SE-EPI where full FOV fast segmented EPI [120-122] is not feasible (as it is with GE) due to insufficient SNR and limited SAR. By reducing the FOV, the number of phase encoding (PE) steps that are needed to achieve the same resolution is reduced. Fewer PE lines results in a reduced acquisition time, however, to simply reduce the phase FOV would result in signal folding into the image.
To reduce the imaging FOV without signal folding, one can use: outer volume suppression [123] (OVS), smaller coils that see a smaller amount of the sample, selective excitation of only the area of interest (inner volume excitation) [124], or multi-channel coils and parallel imaging reconstruction techniques to unfold under-sampled data. These options may also be used in conjunction with each other for further optimization. OVS techniques are straight-forward to implement [125]. However, because of the magnetization transfer effect they result in SNR losses of up to 30% [123] and can be SAR–limited [125]. Parallel imaging techniques and surface coil approaches allow for reduced echo trains/FOVs and are routinely used. However, to arbitrarily reduce the acquisition volume (to achieve readout times which are acceptable) inner volume excitation approaches are ideal. We previously developed and used a 2D inner volume approach for T2 weighted reduced FOV acquisitions (Figs. 3, 5) [28, 126]. In this sequence, a slice-selective 90 degree excitation pulse is followed by a slab-selective (along the PE direction) refocusing pulse. This permits a reduction of the phase FOV (and thus the number of PE lines) and, ultimately, fewer segments and a shorter TR. However, for high spatial resolution applications (i.e., 0.5 mm in plane) in humans at 7T, some segmentation was still needed (3-4 segments compared to full FOV acquisitions that needed 12-16 and in some cases 32 segments [127]). This was prior to the availability of the aforementioned fast head gradients. Currently, using the fast head gradient insert, we are able to achieve 0.5 mm in-plane resolutions with sufficient FOVs, SNR, image quality, and superb functional contrast using single shot 2D EPI with inner volume excitation (Fig. 5). Note, however, that although we achieve such specificity and sensitivity in a single shot, due to inner volume orthogonal RF pulses cross-irradiating images, multi-slice 2D images are not feasible, making the applications of this method extremely limited. As such, the extension of this approach using single-shot 3D GRASE with inner-volume excitation (Fig. 4) [89, 90] provides an enormous opportunity for ultra-high resolution applications at high fields where not only is higher SNR achieved compared to 2D approaches, but the T2-weighted acquisition volumes (depending on the implementation of parallel imaging or multi-slab methods) increase by several fold.
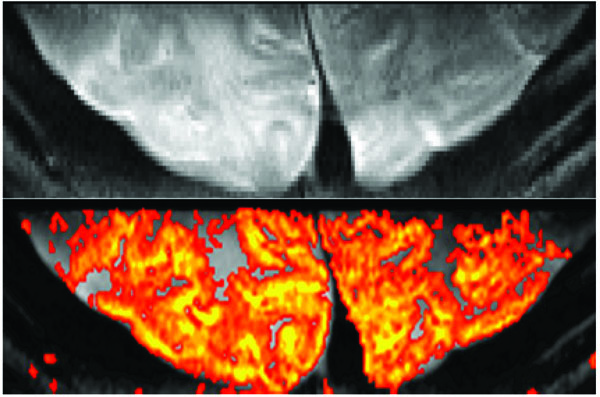
Reduced FOV fMRI. Single Shot SE-EPI with 0.5 mm in plane resolution at 7T (top). Visual activation in humans using a 30 sec on/30 sec off paradigm using a single 8 minute scan and the resulting fMRI map (bottom). Data acquired using inner-volume excitation and a surface coil positioned on the visual cortex. Imaging parameters: matrix: 50 x 256, FOV: 2.5 x 12.8 cm2, resolution: 0.5 x 0.5 x 2 mm3, 35 msec readout TR/TE: 2s/ 50 msec.
With GE imaging,only one RF pulse is played out for each excitation and therefore slab localization is not straight forward. However, as seen in Fig. (1), whole brain coverage using single shot GE-EPI (without FOV reduction) is certainly achievable with ~1 mm isotropic resolutions. Pushing beyond this (i.e., ultra-high resolution) with standard techniques, as evidenced by these images, is on the horizon. Currently, however, the combination of these fast gradients, optimal multi-channel coil designs and ultra-fast acquisition computers, producing images at these resolutions over extended volumes is not common. Ultimately, to obtain ultra-high resolution BOLD images efficiently at any field (but more so at high fields due to the shorter T2*s) typically requires reduced FOV approaches and sacrifices in volume coverage to avoid the long acquisition times (or image segmentation) [12] which result in increases in temporal fluctuations, loss of fMRI temporal dynamics, and inefficient paradigm design. This is especially the case for ultra-high resolution T2-weighted sequences where, due to RF inhomogeneity, SNR varies locally over extended volumes, and SAR can limit efficient whole brain coverage.
SUMMARY
In this paper, we have provided an overview of the current status of high-field and high-resolution fMRI studies for human applications, as well as practical limitations for the acquisition of such data. First, for standard imaging resolution (3 mm), there is little motivation to select a SE-based pulse sequence, since GE fMRI samples the hemodynamic response on this scale and provides much more CNR, while not being limited by SAR or RF field inefficiencies. Additionally, there is little to gain in CNR by taking an experiment with standard resolution from 3T to 7T because of the amplification of physiological noise. However, if high (or extremely efficient) temporal resolution is required, significant gains can be realized for standard spatial resolutions at high fields using slice-accelerated techniques (i.e., multiplexed EPI [2, 128]).
Next, for high resolution (1-2 mm), there are arguments for using either SE or GE pulse sequences. With a GE pulse sequence, some voxels will have spatial specificity of the order of 3-5 mm (vascular blurring); other voxels will have spatial specificity matched to the image resolution. If the neuroscience question will benefit from spatial specificity matched to the voxel size – which will avoid degradation of functional specificity by averaging heterogeneous neural responses – then a SE pulse sequence is preferable. However, the selection of a SE pulse sequence means that high resolution whole-brain coverage would likely not be possible because of SAR and SNR limitations. At 7T the spatial specificity advantage of SE over GE BOLD signals is more significant than at 3T where significant intravascular signals still persist in the SE signal. For this reason along with the relatively low CNR of SE BOLD at 3T, it is unlikely that SE BOLD will provide any advantage over GE BOLD at 3T for any spatial resolution.
Finally, for ultra-high resolution, SE pulse sequences are an obvious choice at high fields. However, due to the limitations of achieving T2 weighting at high fields, reduced fields of view are necessary – both to maintain a reasonable temporal resolution, and because of SAR and local SNR l imitations. Surface coil applications can be used to minimize SAR, allow for higher local SNR, and permit smaller FOVs without signal aliasing, provided that the coil design can provide uniform excitation for 180° pulses over the region of interest. OVS can also be used to reduce the FOV; however, it is more feasible to apply in conjunction with ultra-high resolution reduced FOV GE applications because of SNR and SAR limitations with SE techniques, which have benefited significantly from inner volume approaches. GE BOLD can be used for ultra-high resolution applications provided that there is a priori information about the location of large vessels with respect to the region of interest and that these effects can be avoided either during the acquisition or in the data post-processing. Ultimately, while SE-BOLD and GE-BOLD ultra-high resolution applications tend to be SNR and efficiency limited, they both stand to benefit significantly at high fields such as 7T.
Looking forward, increases in the proficiency of accelerated techniques with more optimized RF coil designs at high field as well as improved gradient performance will continue to mitigate problems related to high magnetic fields. Further, several new pulse sequence options exist which permit even more efficient acquisitions by allowing for 2D accelerations with both 2D [1, 2, 96] and 3D sequences [110], improving the fMRI sensitivity of large volume high resolution applications, where the TR can be limiting due to the large number of slices. With these developments, the potential of higher field fMRI applications will continue to expand in terms of spatial and temporal resolution along with increased volume coverage allowing for functional explorations of the human brain with enormous amounts of detail and specificity.
ACKNOWLEDGEMENTS
Work supported in part by the Human Connectome Project (1U54MH091657-01) from the 16 NIH Institutes and Centers that Support the NIH Blueprint for Neuroscience Research, and by the National Institutes of Health (grants, R01 EY015261 to CAO, R01 EB000331 to EY, P30 NS057091, P41 RR08079), the W.M. Keck Foundation, and MIND institute. The 7 T magnet purchase was funded in part by NSF DBI-9907842 and NIH S10 RR1395.


