Brain-Mind Operational Architectonics Imaging: Technical and Methodological Aspects
Abstract
This review paper deals with methodological and technical foundations of the Operational Architectonics framework of brain and mind functioning. This theory provides a framework for mapping and understanding important aspects of the brain mechanisms that constitute perception, cognition, and eventually consciousness. The methods utilized within Operational Architectonics framework allow analyzing with an incredible detail the operational behavior of local neuronal assemblies and their joint activity in the form of unified and metastable operational modules, which constitute the whole hierarchy of brain operations, operations of cognition and phenomenal consciousness.
INTRODUCTION
Practically all of the major unsolved problems in science today are about complex, self-organizing systems, where vast number of their components interacts simultaneously with each other and where the change in one agent influences the behavior of other [1]. Brain is one example of such natural biologically evolved systems [2-6].
Indeed, “more than 1015 of neurons and about 150 billion of brain cells are connected with one another locally (more than 10,000 direct connections of one neuron with others) in the assembly of structures. These structures in their turn globally communicate with one another through long-distance projections in order to act in a concerted fashion in the construction of the behavior of the large-scale networks. Because the number of distinct brain structures scales proportionally with network size, there are potentially an ever increasing number of structures with which a particular brain structure may need to interact” (see p. 847-848 in Ref. [7]).
This is the so called “elementary basis” of the brain, which enables a very high number of combinations of possible brain states – multivariability of brain functioning [8,9]. Recently neuroscientists are debating how synchronous neural activity within the brain creates such states and orchestrates attention to and perception of objects or scenes, separation of remembered parts of an experience and binding them all together into a coherent whole, thinking and, perhaps, even phenomenal consciousness [10].
There is a growing consensus among researchers that cognitive function arises from dynamic combination of localized operations in specific brain areas and distributed interactions among these operations [11-13]. For this reason, it is hypothesized that the neural correlates of cognition and consciousness must account for the integrated and coherent macro-operation of large-scale brain activity [14]. However, it is not clear how to combine the notions of ‘localization’ and ‘interaction’ in order to best describe how the brain translates physiological operations into mental cognition.
Modern in vivo brain imaging methods of PET, fMRI, Optical Imaging, and EEG (MEG) offer a unique opportunity to explore the neural networks in human brain. However, in order to understand how the brain functions, it is of central importance to map the pattern of the neuronal functional connectivity [15].
Hemodynamically based methods (PET, fMRI, and Optical Imaging) determine functional connectivity by evaluating the correlation in hemodynamic activity between two regions. What is obtained is the information about how such hemodynamic activity in one region is related to that in other regions [16]. However, brain functional connectivity is usually discussed in terms of how neural (electrical) activity in one area is related to neural (electrical) activity in other areas. The neural networks that might be identified on the basis of neural electrical (EEG) interactions and transient brain states are not the same as macroscopic systems identified on the basis of correlated blood flow observed over a variety of brain states [17].
Brain functional connectivity, which is defined as the temporal correlation between spatially remote neurophysiological events [18], is believed to serve as the mechanism for the coordination (or discoordination) of activity between different dynamic cell assemblies across the cortex (for review, see Ref. [15,19]). According to recent interpretations, in the dynamic functional connectivity between such assemblies, the nonlinear interdependence is mostly reflected [5,13,20,21].
In recent years, it has become clear that complex nonlinear time series such as electrical brain activity (EEG) can have extremely complicated behavior [9,21,22]. It has also become clear that standard methods of time series analysis, such as mean power analysis, Fourier transforms with consequent averaging and parametric linear modeling, are generally not exactly adequate in discerning the structure of EEG signals, and may, in fact, lead to erroneous conclusions [23,24]. EEG data indeed appear to have a rich nonstationary and nonlinear structure [5,8,9,21,22], which presumably reflects the current functional state of neuronal masses rather than a random process [24,25] and the processing of an internal mental contexts (top-down processing) [26].
Among the different methodological strategies adopted to study the brain-mind complexity and its expression in the complexity of EEG signal, the so called “Operational Architectonics” (OA) framework [9,7,14,27,28] has received attention, especially due to its good compromise between simplicity, neurophysiologic accuracy, and cognitive plausibility.
OPERATIONAL ARCHITECTONICS OF BRAIN-MIND FUNCTIONING
The initial idea on the frame architecture of brain information processing in rather sketchy form has been originally proposed at the fourth IBRO World Congress of Neuroscience [29] (see also Ref. [30] for a more general presentation). Later it was used mostly as an “umbrella” notion in a series of research [23,24,31-49] leading to accumulation of enormous amount of experimental data which permitted to extensively develop, broaden, and modify the whole conception and establish OA as a theoretical framework in the present form [7,9,14,27,28]. Since then, it has been used to study (a) different brain conditions, such as during cognitive tasks [50], memory [44,51], multi-sensory integration [43], during sleep and drowsy states [36, 52], under the hypnosis [53]; (b) different pathological conditions, such as depression [54], opioid addiction [55], abstinence [56], schizophrenia [57]; and under the pharmacological influence [45,46]. However, despite a lot of empirical studies, the methodological aspects of this approach have been not addressed in a systematic way.
Prior to detail analysis of methodological issuees we would like briefly describe the main upper-level aspects of OA framework and their relation to EEG. The basic idea is that the activity of neuronal assemblies (that form the foundation of OA theory) is “hidden” in the complex nonstationary structure of brain EEG field [8,9]. The main OA postulates are:
- Single neurons (highly distributed along the cortex) can quickly become associated (or dis-associated) by synchronizing their activity/operations and giving rise to transient neuronal assemblies (TNA). TNAs maintain discrete elemental brain operations some of which have phenomenal/subjective ontology in addition to the neuro-physiological one [9].
At the EEG level these operations of the TNAs are reflected in the periods of the EEG quasi-stationary segments (~ milliseconds) within different frequency ranges, registered from different brain locations. The rapid transition processes (RTP) occurring in the continuous EEG activity mark the boundaries between quasi-stationary segments for this activity (Fig. 1). Detail description of this method can be found in Fingelkurts et al. [45,46] and Kaplan et al. [22]. It is assumed that each homogenous segment within a particular EEG frequency band corresponds to a temporary stable microstate in the local brain’s activity, i.e. an operation [14,27]. Because the major contributor to temporal modulation of the variance and power of the EEG signal is the sharp change in its amplitude [58], the identification of RTP can be reduced to the detection of a moment of rapid statistically significant decrease or increase of EEG amplitude.
The identification and statistical approval of a sequence of RTPs (RTPseg tool; BM-Science, Finland) is used for automatic segmentation of the EEG records (for detail description see Ref. [54]). Here we are highlighting only the most important aspects (Fig. 1). The RTPseg method is based on the automatic algorithm of moving double window screening. The ongoing amplitude values in the test window are compared with amplitude values averaged in the level window (test window << level window). If, in accord with the given level of probability of false alert, the value averaged in the level window is exceeded by the highest among the test window value, the time point with the highest amplitude is considered as a preliminary RTP. In order to exclude false alerts caused by anomalous peaks in amplitude, another condition must be fulfilled: the statistically significant difference must be detected between an amplitude value averaged across five time points following the preliminary RTP and the amplitude value averaged across the level window. If these two criteria are met, the RTP is considered as actual. Thereafter, both windows are shifted from this RTP on one time-point, and the procedure is repeated until the whole sequence of statistically proven RTPs is determined [22,43,44].
The identified quasi-stationary segments of EEG activity are characterized by the following attributes [50,46]: A (mV) – averaged across segment amplitude value (reflects the size of TNAs), V (%) – coefficient of variation of within-segmental amplitude values (reflects stability of synchronization within TNAs), L (ms) – length of segment (reflects duration of separate brain operations performed by TNAs), AR (%) – amplitude relation among adjacent segments (reflects either growth (recruiting of new neurons) or distraction (functional elimination of neurons) of TNAs), and S (%) – steepness of RTP among adjacent segments (reflects the speed of neuronal population growth or distraction). These attributes reflect different aspects of local processes in the cortex and thus permit assessing the mesolevel description of cortex interactions (interactions within TNAs) through large-scale EEG estimates [46].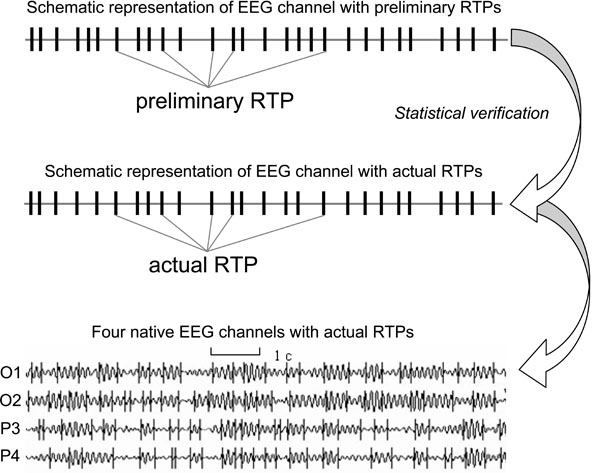 Fig. (1).
Fig. (1).An example of four ongoing EEG channels with rapid transition periods (RTPs) and the schematic representation of one channel (O1) and RTPs (Note that after statistical verification of preliminary RTPs some of these RTPs do not present among actual RTPs). EEG was registered in resting condition (closed eyes) and then filtered in the alpha frequency band (7-13 Hz).
- Temporal synchronization of different brain operations executed by different local TNAs simultaneously (operational synchrony) gives rise to a new level of brain abstractness – metastable brain states [7]. These metastable brain states or functional Operational Modules (OM), as we name them, underlie the realization of brain complex macrooperations: cognitive percepts, phenomenal objects, and reflective thoughts within the operational space-time continuum [14]. Intuitively, the operational space-time (OST) is the abstract space and time which is “constructed” by the brain each time when the particular metastable OM emerges [28]. Formally, the OST means that for a particular complex operation, the spatial distribution of the neuronal assemblies’ locations with synchronous activity at repetitive instants of time (beginnings and ends of simple operations) builds the OM. These distributed locations of neuronal assemblies are discrete and their proximity or the activity in the in-between area, delimited by the known locations, is not considered in the definition (only the exact locations are relevant). Also, between the moments in time that particular locations of the neuronal assemblies synchronize, there can be smaller subset(s) of these locations synchronized between themselves or with other neural locations, though these do not relate to the same space-time of the same OM. The sketch of this general idea is presented in Fig. (2B). Each OM is metastable spatial-temporal pattern of brain activity, because the neuronal assemblies which constitute it have different operations/functions and each does its own inherent “job” (thus expressing the autonomous tendency), while still at the same time been temporally entangled among each other (and thus expressing the coordinated activity) in order to execute common complex operation or cognitive act of a higher hierarchy [14,28]. As has been proposed by Kelso [3] metastability relates exactly to the constant interplay between these autonomous and interdependent tendencies (see also Ref. [59,60]).
At the EEG level the OM phenomenon is expressed in the synchronization of EEG quasi-stationary segments (indexed by Structural Synchrony, ISS) obtained from different brain locations [9,14] and measured by means of RTPsyn tool (BM-Science, Finland). As the details of this technique are beyond the scope of this article (see [54]), we will only concentrate on some essential aspects. The criterion for defining an OM is a sequence of the same synchrocomplexes (SC), whereas SC is a set of EEG channels in which each channel forms a paired combination with high values of ISS with all other EEG channels in the same SC; meaning that all pairs of channels in an SC have to have statistically significant ISS (Fig. 2A). RTP in the reference EEG channel (the channel with the minimal number of RTPs from any pair of EEG channels) is surrounded by a short “window” (ms). Any RTP from another (test) EEG channel is considered to coincide if it fell within this window (Fig. 2A). The ISS for pairs of EEG channels can be estimated using this procedure and a particular mathematical formalism (for details, see Ref. [22,43,44]). The ISS tends towards zero where there is no synchronization between the EEG segments and has positive or negative values where such synchronization exists. Positive values indicate ‘active’ coupling of EEG segments (synchronization of EEG segments is observed significantly more often than expected by chance as a result of random shuffling during computer simulation), whereas negative values mark ‘active’ decoupling of segments (synchronization of EEG segments is observed significantly less than expected by chance as a result of random shuffling during computer simulation).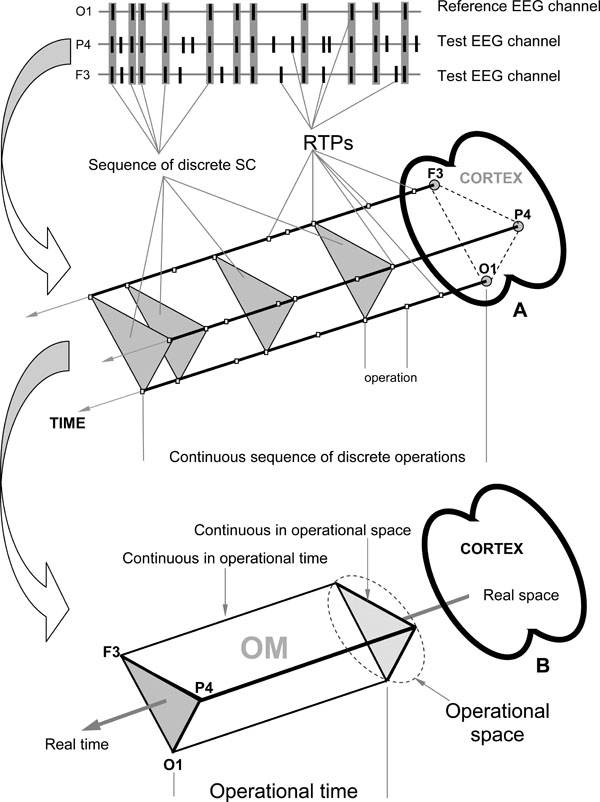 Fig. (2).
Fig. (2).EEG Index of Structural Synchrony. A: Technical estimation of OM. B: Illustration of brain Operational Space-Time (OST). Each OM exists in the OST, which is “blind” to other possible time and space scales present simultaneously in the brain. In the other words, all neural assemblies that do not contribute to a particular OM are temporarily and spatially excluded from the current OST.
- Sequence of these metastable OMs may represent the stream of consciousness [9]. The main idea is that the structure of the electrical brain field (EEG), the structure of cognition, and the phenomenal structure of consciousness, all have the same organization (Fig. 3): the succession of discrete and relatively stable periods (metastable OMs, cognitive acts, or thoughts, correspondingly) separated by rapid transitive processes (abrupt changes between OMs, cognitive acts or thoughts, correspondingly).
- OMs could be operationally synchronized between each other on a new time scale (see Fig. 3A), thus forming more abstract and more complex OM which constitute new and more integrated phenomenal experience [28].
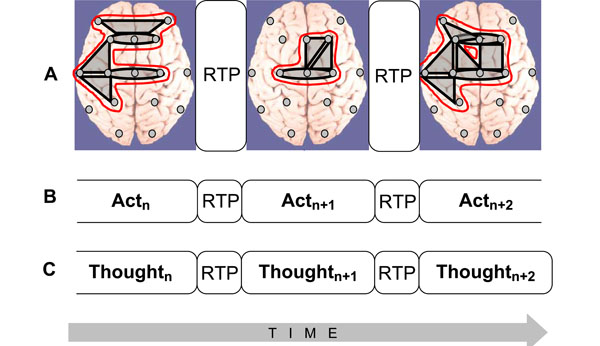 Fig. (3).
Fig. (3).Isomorphism between functional structures of electrical brain field (EEG), cognition, and phenomenological consciousness (reflective thought). A: At the EEG level dynamic structure is presented as a chain of periods of short-term metastable states (or operational modules, OM) of the individual brain subsystems (grey shapes), when the numbers of degrees of freedom of the neuronal assemblies are maximally decreased. Red out-lined shapes (in the on-line version) illustrate complex OMs which are separated by the rapid transition periods (RTPs). B: Changes from one cognitive act to another are achieved through RTPs. Change from one cognitive (and behavioral) act to another is reflected in transitional processes which play the principal role in the organization of cognition. During transitional process the comparison with the parameters of the final result reveals the correspondence between the achieved ‘goal’ and the ‘goal’ that was planned [129]. C: Phenomenological level illustrates the ever-changing stream of thoughts (or mental images) where each momentarily stable pattern is separated by transitive fringes (or RTPs). Consciousness is always changing, but it presents us with a series of substantive thoughts that are themselves momentarily stable [130]. Generally, the description of the cognitive and phenomenological continuum as a chain of the discrete acts (the results of which are achieved due to the simultaneous realization of certain number of operations) coincides with the description of the operational architectonics of the biopotential brain field.
- Also the reverse process is possible: when complex OM (representing phenomenal pattern, object, or reflective thought) guided by attention is decomposed to several simpler OMs which in their turn may be further decomposed even to simpler ones [27].
METHODOLOGICAL ASPECTS
Adaptive Level EEG Segmentation
It is well known that EEG signal is extremely nonstationary [8,22,23]. The understanding of the nonstationary structure of EEG signal is of intrinsic scientific importance because without understanding the character (or nature) of the processes under consideration, the use of many methods of analysis often gives false results. For example, invariants, such as the mean spectrum, average ERP and ERD/ERS, coherency, fractal dimensions, Lyapunov exponents, and others, have a sense only for stationary signal dynamics [61]. Further, the nonstationarity of the EEG process usually does not allow constructing a global dynamical model for the whole observable [62].
Thus, regardless of how powerful or statistically significant the different estimations of averaged EEG phenomena may be, there might be difficulties in the meaningful interpretation of these if they are not matched to their piecewise stationary structure [63-65]. That is why the algorithms based on a nonstationary model of the EEG signal are of a particular importance [22]. However, the conventional parametric (and some other) segmentation procedures [66-68] contain internal controversies and thus have limitations. The main such limitation is that segmentation of the EEG signal into stationary fragments is impossible without construction of an adequate mathematical model, but such a model cannot be built without previous segmentation, since it requires the stationarity for its construction (for detailed discussion and review see Ref. [22], see also [47,48]). To overcome such disadvantages the original framework of the adaptive non-parametric EEG segmentation (together with a corresponding tool-set) was developed. The latest tool (RTPseg; BM-Science, Finland) of the framework’s toolset is used for the purpose (see Fig. 1). This tool is an advanced clean reimplementation of a earlier tool Section [22,43,44]. RTPseg algorithms overcome various numerical limitations that existed in its predecessor and modify and extend its functionality.
In the adopted framework of OA methodology, it is assumed that the EEG signal is “glued” from several segments of random stationary processes with different probabilistic characteristics [48]. In this case, it is possible to consider one quasi-stationary segment as the single event in EEG-phenomenology (Fig. 1). Within the duration of one segment, the neuronal population that generates the oscillations is in the steady quasi-stationary state [47]. The transition from one segment to another reflects the changes of the generator system state or changes in the activity of the two or more systems [66-68]. These transitions (rapid transitional processes – RTP) in the EEG amplitude occurred abruptly and are the boundaries between EEG segments (or brain operations at the functional level; for discussion see Ref. [14,27,28]). RTP is supposed to be of minor length compared to the quasi-stationary segments (Fig. 1), and, therefore, can be treated as a point or near-point [9]. Generally, in the rest condition there may be about 400-600 RTPs per 1-min EEG recording, while during cognitive task this number usually increases and could reach up to 12000 RTPs per 1-min EEG recording [40].
There are few methodological issues, however, regarding the nature of EEG segments that need to be addressed with a more detail. One such issue concerns the validity of RTPs as real markers of the boundaries of quasi-stationary EEG segments. If RTPs are true authentic boundaries of EEG quasi-stationary segments, then the coefficient of within-segment amplitude variability (V) should be substantially higher for the randomly (stochastically) altered EEG when compared with the real (actual) one. Using the procedure of random mixing of amplitude values within EEG signal, the relative V values for stochastic amplitude alternations were estimated for each EEG channel and the result was compared with V values of real (normal) EEG [22]. The V values of the mixed (‘random’) EEG were substantially higher (up to 30%) when compared with the actual EEG. Such an excessive increase in the V values indicates a stochastic processes going in ‘random’ EEG. More precisely, these values represent an estimation of the maximum possible rate of relative alterations in the amplitude variability for a given EEG.
Additionally, if RTPs are true authentic boundaries of EEG quasi-stationary segments, then the coefficient of within-segment amplitude relations between neighboring EEG segments (AR) should be substantially lower for the randomly (stochastically) altered EEG when compared with the real EEG. The analysis indicated that it is indeed the case [49]. Thus, both these tests testify the fact that obtained segments in the actual EEG really have a quasi-stationary nature and reflect the episodes of relative stabilization of neuronal activity within separate neuronal assemblies separated by RTPs.
Application of OA methodology in cognitive experimental design reveals indeed a functional significance of segmental EEG architectonics during both spontaneous (stimulus independent) and induced (stimulus dependent) brain activity [23,32,40-44,53].
However, there is one more important issue to consider in respect to the nature of RTP: if RTPs are the EEG markers of transitional moments between brain operations (which indicate the beginning and end of operations), than, in the experimental condition, the number of RTPs should be much higher exactly at the moment of systematic change from one cognitive/mental operation to another when compared with other time-coordinates or control condition without systematic change of operations. Fig. (4) presents a distribution of time coordinates of RTPs for the three-stage cognitive task and rest condition. As one can see, distribution of RTPs’ time coordinates is not homogeneous during three-stage (20 sec each) cognitive task.
Main peak in the number of RTPs (10-11%) occurred on 19-20 sec – exactly at that moment where was abrupt transition from the 1st stage of cognitive activity to the 2nd one. This increase in the number of RTPs was statistically significant [41]. Transition from the 2nd stage of cognitive activity to the 3rd was also marked by slight increase in the number of RTPs, however without reaching a significant level (Fig. 4). It is important to note here, that second stage of cognitive activity was very different from the first one, but was almost identical to third stage [40]. Therefore, the number of RTPs reflects accurately a systematic change in cognitive operations. In contrast to experimental condition, control condition, which was just rest with open eyes, was characterized by relatively homogenous distribution of RTPs’ time coordinates (Fig. 4). These findings clearly indicate that RTPs are true markers of beginnings and ends of brain-mind operations.
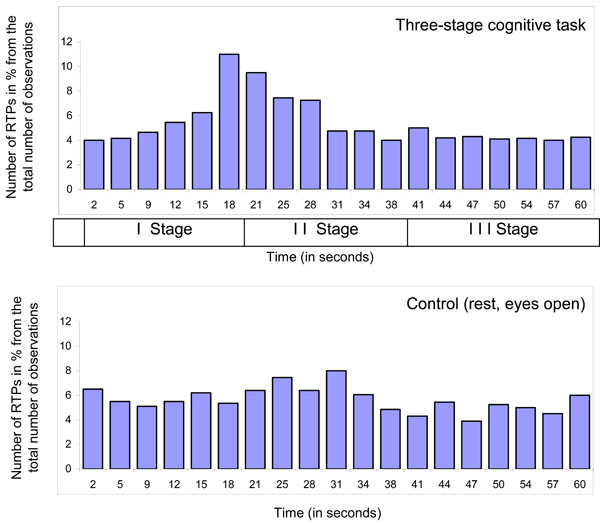
Diagram of time coordinates of rapid transitional periods (RTP) found in different EEG channels for 1-min EEG averaged across all subjects (n = 12), all EEGs (n = 48 for Control condition and n = 131 for Cognitive task) and all EEG channels (n = 8). Explanations are in the text.
EEG Segmental Synchrony as a Measure of Brain Functional Connectivity
Traditionally coherence and correlation [69] has been the main methods to assess the degree of functional connectivity between brain areas [14]. It is interesting that initial idea, advocating the correlation approaches as an attempt to quantitatively describe the relationship in the activity of cortical areas, has gradually transformed into the postulation of the presence of an “interrelation” between different sections of the brain only in the case of a high significance of crosscorrelation and coherency [70]. However, in a strict sense, the coherence value indicates only the linear statistical link between EEG curves in a frequency band [71]. Meanwhile, it is obvious that, in general, the absence of similar types of statistical interrelation between two processes does not mean the absence of any interaction between them at all (for a critical discussion see Ref. [23,32,71]). Show and Simpson [72] also stressed that one must be careful about interpreting coherence (including partial coherence) as an indicator of functional connectivity and pointed out that EEG signals show a finite correlation even when recorded from separate subjects [70].
Recently several new methods for detecting functional connectivity between cortical areas have been published: partial directed coherence [73], dynamic imaging of coherent sources [74], and phase synchrony based on wavelet [75] or Hilbert [76] transforms. However, all these methods have some limitations. The drawback is that these approaches have one or several of the following: they do not take into consideration the nonstationary nature of the data, require long time epochs of analysis, use averaging and smoothing procedures and linear models, which for the brain is not typically the case [61]. For the phase concept to be utilized the frequencies of the signal should be locked, otherwise multiple harmonics of these frequencies may overlap and lead to ambiguous phase information [77]. Further, the concept of phase synchronization can be applied only to homogeneous medium [78], what is an unrealistic assumption for the brain. Additionally, the situation is complicated also by a nonstationary process in the nonlinear phase (de)synchronization measures [79], see also [15].
To overcome the previously mentioned and many other disadvantages, the original framework for estimation of functional brain connectivity – based on the index of EEG structural synchrony (ISS) – was developed (Fig. 2). The latest tool (RTPsyn; BM-Science, Finland) of the framework’s toolset is used for the purpose. This tool is an advanced clean reimplementation of an earlier tool Jumpsyn [22,43,44]. RTPsyn algorithms overcome various numerical limitations of the preceding tool, modifying and extending its functionality.
However, one may question the validity of this structural (or operational) synchrony measure (ISS) as a measure of “synchronization”. The ISS measure is based on the co-occurrence of RTPs between two (or more) EEG channels within the same small time-window, while in physics and mathematics literature “synchronization” is usually defined as ongoing one-to-one functional relationship between two (or more) systems. Hence the usage of term “synchronization” may be not appropriate.
The ISS utilizes explicitly the definition of the inter-area functional connectivity [15,32], which has been agreed upon in the neuroimaging community. According to this agreement [80], functional connectivity is defined as the temporal correlation between spatially remote neurophysiological events [81]. Consistently with this the ISS reflects estimated periods of the mutual temporal stabilization of quasi-stationary segments (spatially remote events) in the multichannel EEG [15]. This implies that, although different neuronal assemblies located in different cortical regions have different anatomical features and superficially appear to have quite different sets of firing states [82] – segregation tendency, they can indeed share, encode, or decode the same information using their own specific anatomy and physiology to develop their own sets of microstates [83] wile still be related to each other by simultaneous rapid transformations – integration tendency [7,9,14,28]. Such coexistence of integrated and segregated tendencies is called metastability [2,3].
The main principle of OA methodology, thus, lies in the moment-by-moment metastable synchronization of the on-going TNAs operations among different cortical areas of the large-scale neuronal networks (for reviews, see Ref. [7,14,23,28,59]). Thus, the ISS index reflects systematic temporal relationship between the activities in different cortical areas (Fig. 2) – synchronization of brain operations (events), which is the essence of functional connectivity (for a review, see Ref. [15]).
This method is very simple conceptually and can be used for any time-series in which we can define events. In principle, when dealing with signals of different character, the events could be defined differently in each time series, since their common cause might manifest itself differently in each time-series (for similar ideas, see Ref. [84]). Since the events in the OA framework are the rapid transitional processes (RTPs) which have some duration (even though very small), their synchronization is estimated between different EEG channels in some time window to capture the temporal duration of these processes. The ISS values have get significant meaning only if there is systematic temporal relationship between two (and more) EEG signals and this relationship is deferent from stochastic level of ISS (ISSstoh).
To arrive at a direct estimate at the 5% level of statistical significance (P < 0.05) of the ISS, computer simulation of RTPs synchronization is undertaken based on random shuffling of time segments marked by RTPs (500 independent trials). These share the properties of the experimental data (number of RTPs in each EEG channel of analyzed pair, number of segments, and number of windows of synchronization), but the time coordinates of RTPs were altered randomly in each trial so as to destroy the natural temporal structure of the data. Generally, repeated random reshuffling of the observed data may lead to a whitening phenomenon [85]. However, in the case of ISS this is unlikely due to the following reasons. The correlation between consecutive time segments marked by RTPs in the raw time series is generally small even if the EEG signal itself is highly autocorrelated in time (see the following section). Moreover, validation of the stochastic level of RTPs coupling was performed on so-called ‘surrogate’ EEGs [40] in which a mixing of actual EEG channels was done in such a way that each channel was recorded in a different time, so that the natural time relations between channels in such multichannel EEG were completely destroyed. However, the number and the sequence of segments within each channel remained the same as in the actual EEG. The values for stochastic level of RTPs coupling were almost the same in both procedures and were equal to zero. Thus, the approach of random shuffling of EEG segments is justified. However, other approaches are also possible (see for example Ref. [85]).
As a result of this procedure, the stochastic level of RTP coupling (ISSstoh), and the upper and lower thresholds of ISSstoh significance (5%) are calculated. Thus, only those values of ISS that exceed the upper (active coupling) and lower (active decoupling) thresholds of ISSstoh have been assumed to be statistically valid (P < 0.05). The ISS tends toward zero where there is no synchronization between the EEG segments, or has positive or negative values where such synchronization exists (Fig. 5). Positive values indicate ‘active’ coupling of EEG segments (synchronization of EEG segments is observed significantly more often than expected by chance), whereas negative values mark ‘active’ decoupling of segments (synchronization of EEG segments is observed significantly less than expected by chance).
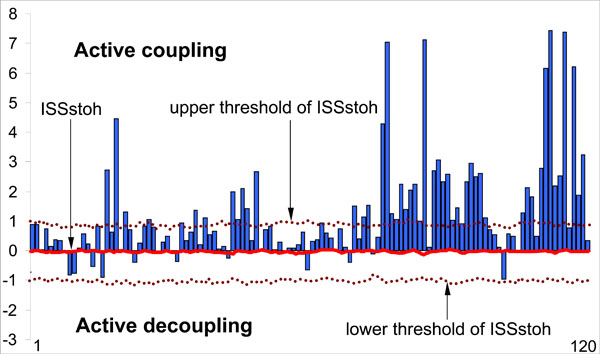
Schematic illustration of the index of structural synchrony (ISS) and its stochastic levels. As an example, the calculations of ISS are shown for 16 EEG channels. The Y-axis displays the ISS values found in the experiment (illustrated as bars). The X-axis displays the 120 possible pair combinations of 16 EEG channels (1 = O1-O2, 2 = O1-P3, 3 = O1-P4, ... 118 = Fz-F7, 119 = Fz-F8, 120 = F7-F8). The data presented for a healthy subject in rest condition, eyes closed. Figure is modified from the Fingelkurts et al. 2004, Human Brain Mapping©.
The above description of EEG structural synchrony measure and its relation to functional connectivity and underlying neural substrate satisfies the main requirements of Horwitz [80] for the usage of functional connectivity concept. Even though generally the measure of functional connectivity does not require any model [86], we believe that to go further in the interpretation of experimental data, computer modeling of OA framework has to be assessed in the future.
ISS Reshuffling Procedure Validation
The method of reshuffling EEG segments to generate full EEG recordings under the null hypothesis solves the problem of specifying a sampling distribution when the law of the time length of EEG segments is not known. But this method has an implicit assumption: the independence (or lack of autocorrelation) between the length of each segment (i.e. the length of segment n should not be correlated with the length of segment n-1). The presence of autocorrelation will lead to an excess of falsely described connections.
The Fig. (6) presents two samples of autocorrelation for lengths of EEG segments obtained from the occipital (O1) and frontal (F4) cortical areas during 20 min of EEG recording (for one subject). Even though there is small decrease of correlations with increasing lag, it never reaches statistically significant level and thus should be considered as irrelevant. Note that with the exception of lag 0, which is always 1 by definition, all other autocorrelations fall below the 95% confidence limit. Thus, we may conclude that adjacent lengths of EEG segments (defined by RTPs) do not co-relate significantly. However, this result should be regarded as a preliminary test, considering that strictly speaking, the use of the autocorrelation function for this purpose is not absolutely correct, because (a) the key assumption underlying such statistical analysis is the “stationarity” of the registered signal, while the EEG is a highly nonstationary signal [9,22]; (b) the lengths of EEG segments (observations) are not equispaced; although the time variable is not used in the formula for autocorrelation, the assumption is that the observations are equispaced; and (c) the sequence of EEG segment lengths does not strictly correspond to the time series.
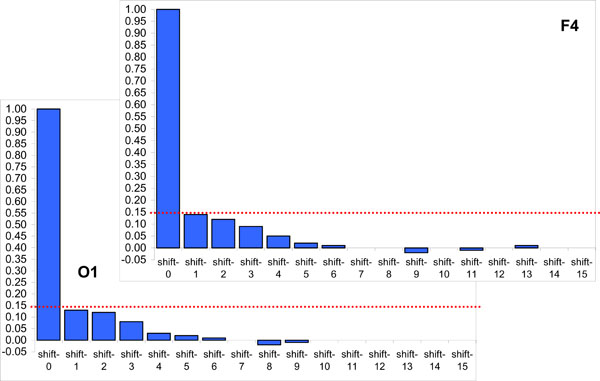
Two samples of autocorrelation for lengths of EEG segments obtained from occipital (O1) and frontal (F4) cortical areas during 20 min of EEG recording (1 subject). Y-axis, Autocorrelation coefficients; X-axis, Time shift/lag (1, 2, 3, ...). Horizontal doted lines indicate the 95% confidence level. Figure is modified from Fingelkurts et al., 2007, Human Brain Mapping©.
Besides the limitations mentioned above, the number of theoretical considerations (based on experimental results) supports the fact that different segments of EEG should be relatively independent: each of these quasi-stationary segments is formed by a random stationary process with particular probabilistic characteristics which remain relatively constant within a segment and which changed abruptly from one segment to another [83] (for review, see Ref. [23,48]). The transition from one segment to another reflects changes in the generator system state or changes in the activity of the two or more systems [23,37,47]. Therefore, in either case, we may conclude that adjacent lengths of EEG segments do not correlate.
ISS and Normalized Version of ISS
Although being quite informative, the ISS will be dependent on the global density of RTPs in the analyzed EEG epoch even under no real connectivity between EEG channels. Therefore one may think that it might be desirable to develop or improve the ISS to a normalized version.
The normalized version of ISS (ISSn) can be easily calculated. Fig. (7) presents comparison of the ISS and ISSn values. It is obvious that both indices lead to the same qualitative results (Fig. 7). The coefficient of correlation between ISS and ISSn equals 1 (P < 0.0001). This equality revealed an important feature of the synchronization index based on RTP coupling: the ISS measure is already normalized since the parameters of the formula take into account the global density of RTPs in each EEG channel within the analyzed EEG epoch.
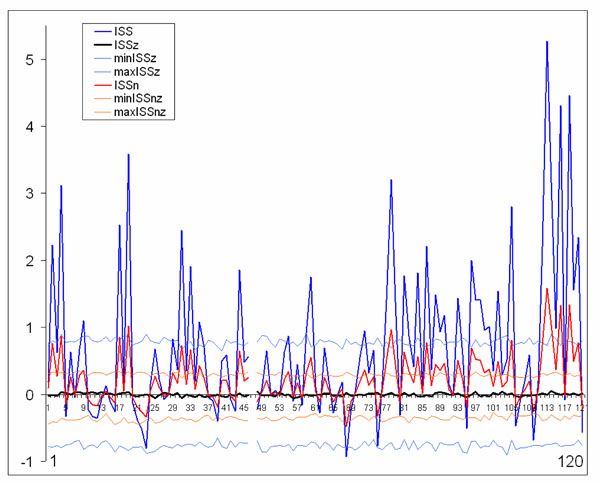
Schematic illustration of index of structural synchrony (ISS) and its normalized version (ISSn) with each own stochastic levels. As an example, the calculations of ISS and ISSn are shown for 16 EEG channels. The Y-axis displays the ISS and ISSn values found in the experiment. The X-axis displays the 120 possible pair combinations for 16 EEG channels (1 = O1-O2, 2 = O1-P3, 3 = O1-P4, ... 118 = Fz-F7, 119 = Fz-F8, 120 = F7-F8). ISSz indicates the stochastic mean values of structural synchrony obtained during the computer simulations; min/max ISSz indicate the stochastic levels for ISSz; normalized min/max ISSnz indicate the stochastic levels for the normalized ISSnz. A line representation was chosen instead of bars for ease of comparison. Figure is modified from Fingelkurts et al., 2007, Human Brain Mapping ©.
The only difference between ISS and ISSn measures is the significantly lower values for ISSn (Fig. 7). This is precisely why it is recommended to use the ISS index: the higher values give more room for their variability; and this is an important attribute of any index to be used in practical experiments, when one needs to distinguish statistically between two (or more) conditions.
Stability of ISS
There may be a reasonable question on whether this new type of EEG synchronization is genuine and not just an artifact of the ISS method. One may think that the best approach to test this is through measure EEG synchronization in several different ways and show that the increased (or decreased) functional connections are indeed robust.
It is well established (for discussion, see relatively recent paper of Horwitz [80]) that multiple ways by which functional connectivity can be determined may lead to different conclusions about whether two brain units are strongly interacting with one another. For example, it has been shown that the value of EEG coherence can be low even when the phases of two EEG channels are synchronized [75]. Most likely, different measures of functional connectivity are not related to one another in any kind of simple way and sensitive to different aspects of interregional interactions. Thus, comparisons of functional connectivity from different measures are not trivial and should be done with caution [80].
In this sense, the best way to obtain the robustness of ISS measure is to check ISS values on homogeneity. Homogeneity means that the rules governing the changes in ISS values are the same throughout the whole experiment(s). Testing may be accomplished by several ways: when subjects underwent the same experiment with the same instructions twice (the test-retest reliabilities); by splitting a whole EEG data into two or more parts and analyzing these separately; or by using a double-blind, randomized, cross-over study. Here we will describe the results of splitting test of ISS data. The question on which we are going to answer is whether the ISS values characterize the majority of the trials analyzed? If this true, the homogeneity of ISS data should be obtained. By definition, homogeneity can be assumed when all subparts of the data and the total data yield the same result [87]. This would mean that the data is robust and that they are not the artifact of the method.
The ISS profiles for pair-wise coupling (120 possible pair combinations available from the 16 EEG channels) were estimated and compared for five, ten, twenty, and sixty seconds of the same EEG (for a particular and always the same stage of a memory task; see Ref. [44]). The ISSstoh and its upper/lower thresholds (distribution of ISSstoh values) were estimated also (see above).
Fig. (8) illustrates this analysis. One can see that the noticeable profile of ISS values already exists at 5-s EEG interval, and that this profile remains almost identical to the profile of ISS values for the whole 60-s EEG interval (which corresponds to sum of all trials of the same stage of a memory task). The main positive peaks (which correspond to concrete EEG pair combinations) coincide precisely in the 5-s and 60-s EEG ISS profiles (Fig. 8). Although we cannot be sure about the statistical significance of all ISS values in 5-s profile, because many of them lay inside the threshold of ISSstoh, it is important that the main peaks of the ISS profile for 5-s EEG intervals coincide precisely with the main peaks of 60-s EEG intervals (where they all reach statistical significance).
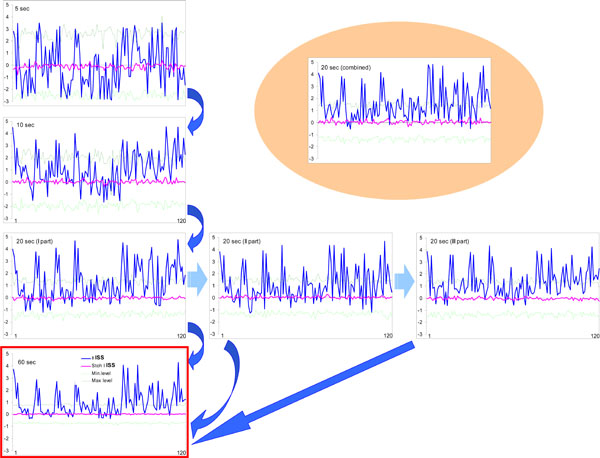
Index of structural synchrony (ISS) of cortical alpha activity for different time intervals. The Y-axis displays the ISS values. The X-axis displays the 120 possible pair combinations of 16 EEG channels (1 = O1-O2, 2 = O1-P3, 3 = O1-P4, ... 118 = Fz-F7, 119 = Fz-F8, 120 = F7-F8). A line representation was chosen instead of bars for ease of comparison. Explanations are located in the text. Figure is modified from Fingelkurts et al., 2003, NeuroImage©.
The values of the ISS profile for the 10-s EEG interval are already more stable (statistically) and majority of main peaks reach the level of statistical significance (Fig. 8). Additionally, one can see that the first, second, and third 20-s EEG intervals do not differ from each other significantly (correlation coefficient: CC = 0.97, P < 0.05 for I-II; CC = 0.87, P < 0.05 for I-III; CC = 0.81, P < 0.05 for II-III) and are very similar to the whole 60-s EEG ISS profile (CC = 0.84, P < 0.05). Moreover, all pair combinations which exceeded the stochastic threshold are the same for each of 20-s EEG intervals as well as for the whole 60-s EEG epoch (Fig. 8).
Thus, results obtained in this analysis show that the functional connectivity between EEG channels is stable and characterizes the vast majority of the analyzed trials. The evidence became stronger if we take into consideration the results of analysis of the 20-s EEG interval, which was artificially constructed from 1-s EEG intervals taken 20 times randomly during the 60-s EEGs belonging to the same stage of memory task (see Fig. 8). The values of such ISS profile are very similar to any other 20-s EEG ISS profile (CC = 0.88, P < 0.05; CC = 0.92, P < 0.05; CC = 0.81, P < 0.05; correspondingly to I, II and III 20-s EEG intervals) and almost the same as the analogous values of ISS profile for the 60-s EEG (CC = 0.78, P < 0.05). At least all peaks, which exceeded the threshold of analysis, coincide precisely (Fig. 8).
Thus, the splitting-test reliabilities (estimated by CC) of the ISS values between the different parts of data were very high; and this confirms the validity of the functional connectivity estimated by ISS. Reliability measures minimize both Type I and Type II errors and eliminate the need for multiple comparisons correction because by definition chance findings do not replicate [88].
EEG Epochs and ISS
Prior to estimation of ISS, each individual EEG recording is arbitrarily divided into number of epochs of a particular duration. There are two potentially important issues here to consider. First, are the different n-min EEGs from the same individuals as different as n-min EEGs from different individuals? If not, then such EEGs cannot be considered as a sample of independent observations, and the Wilcoxon test to asses the differences between experimental groups is not the best choice. Second, the division into n-min epochs is arbitrary; depending of the epoch length used, the degrees of freedom available to the Wilcoxon test will vary, as will probably the results as well.
Statistically, different epochs of ongoing EEG within one subject may be considered as independent observations (imagine that we made 10 independent 1-min EEG recordings) since they are not coupled to any particular internal physiological processes and/or external stimuli. Physiologically, the EEG epochs from the same subject are, naturally, more dependent than epochs from different subjects. This is the general problem of practically all EEG studies. However, the question is: whether the difference in variability of EEGs from the same and between different subjects is significant. The most general parameter which describes EEG is its power spectrum.
Unfortunately, the averaged power spectrum which is used in most of EEG research is prone to many limitations and presents at most a virtual estimate [89]. To assess the appropriateness of the general description of 1-min EEG epochs, we calculated the probability-classification profiles (PCP) of short-term spectral patterns (method described in Ref. [90]) and compared them within and across the subjects for the same condition. To assess stability of this measurement during each 1-min EEG epoch within each subject and across subjects, we calculated the coefficient of variability (CV = standard deviation / mean) as a first measure of stability for averaged PCPs across all 1-min EEGs separately for each channel for each subject and for all subjects together. Further, data were averaged across all EEG channels for each subject and for the group of all subjects. PCP was presented as the histogram of the relative presence of each spectral pattern type for a particular EEG [90]. Analysis of all PCPs for all subjects revealed that EEGs of all subjects were dominated by alpha activity (spectral pattern had dominant peak around 10 Hz) for the same condition. The coefficient of variability demonstrated that this type of activity was stable (a) within each subject (CV ranged from 0.4 to 0.6 for different subjects) and (b) across the subjects (CV = 0.6). Although EEGs within subjects were somewhat more similar to each other than across subjects, the interindividual variability was only insignificantly higher, and was still relatively low. Thus, stability of EEGs within and between subjects was very similar for the same condition. These facts justify the pulling of all data together and the analysis of all 1-min EEGs in the common pool. The same is true for any n-time EEG epoch.
The division of the EEG into relatively small 1-min intervals provides a relatively large number of analyzed epochs; it is important that an unbiased estimate of the synchronicity index is computed using enough data samples. Such an approach is justified because there are no fixed positions in the EEG, and one can therefore divide it into any number of epochs with a length appropriate for the particular experiment and analysis.
In previous section it has been shown that the reliable synchronicity profile already exists at 5-sec EEG intervals, and remains almost the same as for the whole 1-min EEG. The first, second, and third 20-sec intervals of the 1-min EEG did not differ from each other significantly and also strongly resembled the whole 1-min EEG profile. These results showed that the functional relationships between EEG recordings are stable and do not dependent on the analyzed epoch (beyond 5-sec). An increase of EEG epoch beyond the 1-min interval does not lead to any changes in the synchronicity profile [40]. Therefore, the results of ISS measure do not significantly depend on the epoch of EEG analysis.
Problem of Multiple Comparisons and ISS
Separate computer maps of the ISS values are created for each subject and for each n-min EEG epoch of analysis. The problem of multiple comparisons between maps cannot easily be overcome due to the large number of possible pairs of functional connections [91]. This problem is common to all studies that require multiple comparisons between maps [92,93]. To ensure valid results, the pairs of functional connections considered relevant for the further analysis if they consistently appeared in most of the analyzed EEG epochs and subjects (85-100%) for the same experimental group (or condition). However, the question remains whether a frequency of appearance higher than 85% will depend on the potential effect of multiple comparisons.
Simple calculations enable us to clarify the situation. In most of studies 20 EEG derivations are used. We will use this number as an example. If there are 20 EEG channels, then in total there should be (20*20-20)/2 = 190 pairs of combinations of EEG channels (electrodes). Thus, we can expect 190*0.05 = 9.5 false positives (on average) for each single n-min EEG analyzed under the null hypothesis (where 0.05 is the significance level). Based on these calculations, it is rather improbable that, a false-positive functional connection will emerge by chance 85% of the time.
Therefore, the level of frequency higher than 85% is appropriate. However, this conclusion relies on the following two assumptions: a) the nominal 0.05 is correct (so it is crucial that no significant autocorrelation exists between the lengths of EEG segments) and b) the n-min EEG epochs within individuals are as different as those between individuals. As it was shown in previous sections, these two assumptions are valid. Thus, we may conclude that with the threshold of 85% there is no need for multiple comparison correction.
Problem of Volume Conduction and ISS
It is often claimed that volume conduction is the main obstacle in interpreting EEG data in terms of brain connectivity [94]. Although many methods for estimation of functional brain connectivity are clearly contaminated by volume conduction, we have shown in modeling experiments that the values of the ISS are sensitive to the morpho-functional organization of the cortex rather than to the volume conduction and reference electrode (for relevant details, we address the reader to Ref. [22,40,49]). Here we will describe only main results of modeling experiments.
The ISS topological variability was studied in the pairs of EEG channels recorded from longitudinal (occipital-to-frontal) and transversal (posterior and anterior left-to-right) electrode arrays (in straight and backward directions) with a dense electrode positioning (Fig. 9). The relationship of the ISS versus interelectrode distance was analyzed [22]. Also data from actual EEG was compared with so-called ‘surrogate’ EEG in which a mixing of actual EEG channels was done in such a way that each channel was recorded in a different time. Thus, the natural time relations between channels in such EEG were completely destroyed. However, the number and the sequence of segments within each channel remained the same as in the actual EEG. The ISS values obtained from the ‘surrogate’ EEG indicate the relative rate of stochastic alternations (confidence levels) of ISS in the actual EEG [40]. Based on the volume conduction model, assuming that there is spatial homogeneity in a non-connected system, one would expect the ISS values to exhibit a smoothed decrement with increased interelectrode distance. Moreover, this decrement should be equal for a posterior-to-anterior versus anterior-to-posterior directions. Indeed, we demonstrated that the ISS decreased with the increasing of the interelectrode distance. However, the relationship between the ISS and interelectrode distance was very far to be monotonous [22]. In contrast, previous studies measuring EEG coherence pointed to a clearly monotonous decrease of coherence values with increasing interelectrode distance [71]. It is important to note that practically all ISS values in this study were significantly higher (p < 0.05 to p < 0.01 for different pairs, Wilcoxon test) than the stochastic level of synchronization in the ‘surrogate’ EEG. This notably indicates that even on maximal interelectrode distances there was substantial synchrony between the structural peculiarities of electrical field.
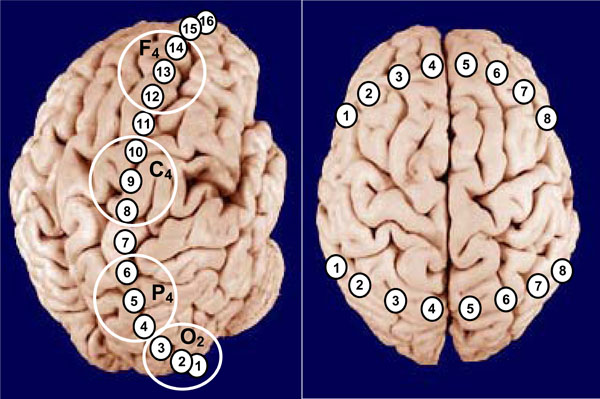
Schematic illustration of positioning of longitudinal (posterior-to-anterior) and transversal (posterior/anterior left-to-right) EEG electrode arrays. Large white circles indicate the classical areas of EEG recordings in accord with International 10-20 System. Explanations are in the text.
We also found that straight (posterior-to-anterior) and backward (anterior-to-posterior) dependences of ISS from the interelectrode distance were significantly different between each other. The ISS decrease for the straight direction was significantly faster (p < 0.05) than for the backward direction [22]. This so-called “spatial hysteresis” obviously pointed to a conclusion that ISS reflects morpho-functional peculiarities of the different cortical areas and is indicative of a non-isotropic nature of the cortex electrical field, rather than it reflects the process of volume conduction of the electrical field in the brain tissue. If ISS would really reflect only volume conduction, changes in the values of ISS should have been equal for the same distances, regardless of which brain areas are involved. Clearly, they are not [40].
In the study of ISS dependence from the interelectrode distance in the transversal arrays it has been shown that although ISS values were slightly dependent on the interelectrode distance, the highest values of ISS were obtained for cortical areas with maximal interelectrode distance – homological (electrode 1 and 8 at the Fig. 9; see also [22]). It is supposed that homological cortical areas usually participate in the same functional acts [14,40].
Taken together, the findings obtained in these studies suggest that ISS has notable topological peculiarities along the neocortex, and thus, is sensitive to morphological and functional organization of the cortex [22].
In order to compare the results of EEG structural synchrony (SS) approach with some of conventional methods, the Pearson coefficients of correlation were calculated for the same data [22]. Although the results of crosscorrelation analysis and analogous data for ISS were similar, the SS description of interrelations between cortical areas was significantly more contrast and pronounced. The same rule was found when the interelectrode distance was taken into consideration [22,40]. The similarity between dynamics of ISS and crosscorrelation values was observed only for the rest conditions. However, in the cases of a more complex structure of the electrical field architectonics (during cognitive tasks or pathological states), the dynamic characteristics of ISS and crosscorrelation indices may be substantially different [49]. The obtained results pointed to a conclusion that most likely exactly the temporal consistency of EEG segmental structure initially underlies and determines high values of crosscorrelation and coherence [22].
It is important to stress that contrary to other EEG measures of functional connectivity, the ISS measure is reference-independent [40,49] and no implicit or explicit source model is needed for the interpretation of the results.
In fact, volume conduction should lead to spurious correlations which would be equally represented across all frequency bands and would be just as likely to be positive as negative. As our modeling experiments showed, the contribution of these spurious results to the overall picture seems likely to have been largely insignificant: a) in contrast to coherencies which are largely redundant in neighboring channels [95], the ISS measure is not [22]; b) adding noninteracting sources (e.g. noise) to EEG signals causes a decrease in the ISS measure instead of an increase, thus leading to an underestimation of ISS effects, rather than generating spurious ISS values [40].
Given that actual correlations occurred with a much higher incidence than expected by chance, and due to the independence of ISS from the power spectrum of the EEG signal [23,44], we believe that the ISS measure can accurately reflect cortical functional connectivity. The accuracy of topographic EEG mapping for determining local (immediately under the recording electrode) brain activity was already established by Cook et al. [96]. Giving further support of the interpretation that the electrophysiological differences reflect differences in brain functioning is that the ISS measure was specifically developed to measure dynamic interdependencies between rapid changes in time series and to be applied to test a specific hypothesis that such functional correlations are different in various functional states [23,43-46,53] and diseases [40,49,54-57]. We therefore argue that the ISS measure is virtually unaffected by volume conduction and has construct validity in the presented context.
Interfrequency Coupling and ISS
Considering the composite polyphonic character of the EEG signal, one needs keep in mind that frequency heterogeneity can influence the segmental structure of the EEG signal [23,40]. Precisely discrete frequency components play the main role in ‘switching on’ and ‘turning off’ of discrete morpho-functional operations of brain systems [7,12-14,28,33,40].
It is worth to note here that methodologically within the OA framework there are no restrictions for the relations between frequency bands, because the ISS measure does not associated with the phase relations of the EEG signal as it is the case for other conventional techniques for estimation of EEG synchronization [23]. Application of OA methodology reveals that segmental flows for each of the EEG frequency component are more or less synchronized, depending on the character of the information-processing of brain activity [40]. Interesting, such synchrony does not depend on the frequency bands’ closeness in the EEG spectral pattern [40]. One can see from Fig. (10) that ISS was not always higher, for example, in the pair alpha1-alpha2 of frequency bands (neighbors) when compared, for example, with the pair delta-beta1 of frequency bands (non-neighbors).
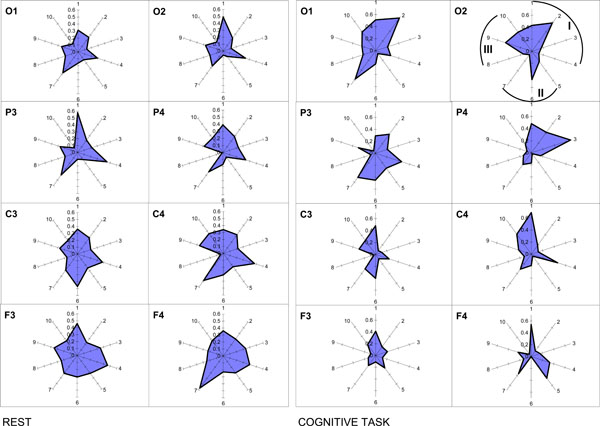
Nonrandom ISS values for ten pairs of five main frequency bands. The radian-axis displays the labels of the frequency band pair connection. The median-axis displays the average values of ISS for the frequency band pair connection within each category. Sections I, II, and III of polar diagram correspond to the frequency band pair connections grouped on the basis of closeness of frequency bands to each other in the power spectrum. I section contains all neighboring pairs of frequency bands: 1 – delta-theta; 2 – theta-alpha1; 3 – alpha1-alpha2; 4 – alpha2-beta. II section contains pairs of frequency bands which are separated by one band: 5 – delta-alpha1; 6 – theta-alpha2; 7 – alpha1-beta. III section contains pairs of frequency bands separated by two and more bands: 8 – delta-alpha2; 9 – theta-beta; 10 – delta-beta.
The principal finding is that the ISS of basic EEG rhythms decreased with the increase of cognitive loading [40]. Another finding concerns the occipital-frontal gradient: ISS values for the interfrequency synchrony increase during rest condition in the direction from occipital to frontal cortical areas and decrease during cognitive activity (Fig. 10). Interesting, this phenomenon does not depend on the EEG alpha-activity expression, since it was identically present in subjects with very high and very low alpha-activity [40].
Operational Modules of OA and Spatiotemporal Patterns of other Frameworks
From the first sight, there is some correspondence between operational module (OM) of OA framework and spatiotemporal EEG patterns described in other theoretical frameworks: the functional clusters of Tononi and Edelman [97]; holoscapes (spatiotemporal EEG patterns of cooperative processes) of Pribram [98]; and quasi-stable EEG spatial structures of Nunez [99]. Although all these modules have much in common, the differences between them come from the particular method of their estimation (see the following section). OMs are based on the estimation of ISS values among involved EEG channels (Fig. 2). Structural EEG synchrony (indexed by ISS) refers to a general class of nonlinear interdependencies between dynamic systems, in which rapid transients in one system can be directly mapped to a second system [22]. In general, this measure belongs to the class of methods estimating synchronization behavior between nonidentical (structurally nonequivalent) systems (for a detailed discussion on this and other classes of synchrony methods, see Ref. [100]).
The main benefit of the OA methodology over the ones quantifying coherence, correlation, and phase synchronization is a methodological-conceptual one. Contrary to findings of previous EEG studies on functional connectivity, the ISS measure is well suited to extract information about discrete brain operations from EEG recordings and to estimate the level of inherent synchrony of these operations appearing simultaneously and locally in different cortical areas (for further discussion, see Ref. [14,15,28]). It can therefore quantify a broader range of coordination phenomena, especially metastable and nonstatic nonlinear phenomena, which cannot be captured by phase synchronization-based metrics [101]. Phenomenologically, this type of EEG structural synchrony corresponds to the operational synchrony process: transient synchronization of operations executed by distant transient neuronal assemblies [9,14,27,28].
It has been demonstrated that if two areas of cortex are operationally synchronized, then they tend to be also synchronized with some other areas [40]. Calculations showed that the power-law statistics governs the probability that a number of cortical areas are recruited into an OM. This ubiquitous dependency is characterized by a fractal relation between different levels of resolution of the data, a property also called self-organized criticality [5,102].
Additionally, as we have shown somewhere [15], OMs are not directly connected with the structural (anatomical) modules of the cortex [103]. It should be stressed also that discussed OMs are very distant from static functional modules (FM). According to FM model, each function is allocated to an element of the brain system – FM, and features of external stimuli are directly mapped to each FM. In contrast, the OMs within the OA framework have dynamic behavior – they are metastable [7,14,28]. So the function of each element cannot be uniquely determined (see also Ref. [104]). This is in line with work of Ramachandran and Blakeslee [105], who found evidence of considerable changes of FMs; and it is in support of the concept of a dynamic brain [4].
OMs which are proposed in the OA framework are the brain field characteristic and might offer some advantages over physical connections, as considered briefly in Nunez [99] and in the work of Hoppenstead and Izhikevich [106], who found that the synaptic connections between cortical columns did not guarantee substantial interactions. In resent publication, John [107] also argues that brain electromagnetic field might be that phenomenon where we must search an emergent property of mentality. This idea has initially received substantial support from EEG studies of Lehmann and colleagues [83,108], which have demonstrated that the dynamics of the whole brain EEG field can be represented by the intervals of quasistability (or “microstates”) and by sudden transitions between them [109,110]. Furthermore, it has been shown that these microstates are associated with different modes of spontaneous [111] and abstract [112] thoughts, and with spontaneous visual imagery [112].
However, because Lehmann’s segmental methodology is based on the momentary whole brain electric field configurations, it does not provide information about frequency domain. In such a case the relationship between microstates and frequency oscillations remains unclear. Another drawback of Lehmann’s approach concerns the involvement of different cortical areas: even though the whole spatial brain electric field segmentation is a very important method for studying the quasi-stationary structure of brain activity, it is, however, lacking of the time-dimensional information in each cortical area separately. Moreover, local EEG sites do not participate equally in the formation of the resulting microstate and this has not been justified from the viewpoint of indubitable neurobiological equivalence of cortical areas.
In contrast to Lehmann’s spatio-temporal EEG field microstates, OMs have very reach internal structure, where the temporal information of each cortical area (which participated in OM) is precisely known and preserved (see Fig. 2); additionally such OMs can be formed within any frequency band and even between different frequency oscillations [40]. In this sense, OMs lie in between the classical and connectionist architectures. From the one side they resemble connectionist networks [113] in many respects: OMs may serve as associative, content addressable memories, and they are distributed across many neural assemblies. Yet, from another side, the specific temporal patterns (OMs) by themselves are unitary, like symbols of classical logics [114]. Thus, within the same OM, discreteness of parallel brain operations (indexed as sequences of concatenated quasi-stationary segments in local EEGs) is implemented in the continuity of unified metastable spatio-temporal patterns (indexed as OMs) of brain activity [28].
Interesting, the mean duration (life-span) of OMs (for an EEG with a broad frequency band of 0.3-30 Hz), which cover most part of (or entire) cortex usually equals to 80-100 ms. These values coincide precisely with the mean microstate duration of entire neocortex (82 ± 4 ms) obtained for healthy young adults using Lehmann’s approach [115]. These results cross-validate both methodologies.
Relation of OA Framework to other Theoretical Models
At the first sight, the OA theoretical framework has some resemblance to other theoretical accounts currently dominating the field of brain-mind research. Here we will briefly discuss the similarities and differences between OA and other theoretical frameworks. One such theory is the “Global Workspace” (GW) framework [116]. According to it, the brain seems to show a distributed style of functioning, in which the detailed work is done by millions of specialized neural groupings without specific instructions from some command centre. Mostly these are unconscious processes; however, consciousness creates widespread access (free from interference) to complex and unconscious systems. Using “theater metaphor,” Baars argued that as theatre combines very limited events taking place on stage with a vast audience, consciousness involves limited information that creates access to a vast number of unconscious sources of knowledge [117]. One can see that the OA theory has some similarity with Baars framework.
Generally, the OA framework is also consistent with the “Framework for Consciousness” suggested by Crick and Koch [118]. The main lines of correspondence are the following: a preamble on the cerebral cortex; the fact, that most cortical areas is sensitive to correlations among correlations being expressed by other cortical areas; the importance of neuronal assemblies; the claim that conscious awareness is a series of discrete snapshots and that the durations of successive snapshots are not constant [118].
Further, the OA theoretical framework is also compatible with Chalmers’ “Philosophy of Mind” [119] in the part that any distinction in experience should be mirrored by a distinction in neural activity, and the pattern of experience should be matched by the pattern of awareness (see “functional isomorphism” principal in Ref. [7,9,27]).
The OA framework is also consistent with Revonsuo’ “Neuroconsciousness” conception [120]. According to this framework, consciousness is a real biological phenomenon that is physically located within the brain; – it is the phenomenal level of brain organization [121]. Further, it is suggested that physiologically neuroconsciousness consists of large-scale electrophysiological (or bioelectrical) activity spatio-temporal patterns; and synchrony in these patterns may be the mechanism by which the conscious state and its contents are realized in the brain. Further, it has been proposed that “neural synchrony seems to be capable of supporting higher-level electrophysiological entities that resemble the content of the phenomenal level of organization” (p. 6 in Ref. [120]).
However, the OA framework, by contrast to other theories, is not just a conceptual construction, – it has methodological means to explicitly measure, estimate, model and describe the brain-mind operations involved in the complex human behavior, cognition and phenomenal consciousness. According to the OA framework, the notion of operation is central for perception, attention, intention, memory, action, and eventually consciousness [14,27].
Besides mentioned above theories, there are two related theoretical frameworks which have the closest similarities with the OA conceptualization. These are (1) the “Resonant Cell Assemblies” framework developed by Varela [122] and (2) the “Dynamic Core” theory proposed by Tononi and Edelman [97]. Because of limited space, we summarize the similarities and differences between these theoretical frameworks and the OA theory in Table 1. One can notice that besides similarities between all three theories, the OA framework has several notable differences. We will concentrate here only on the most relevant ones:
Comparison of Operational Architectonics framework with Resonant Cell Assemblies and Dynamical Core frameworks.
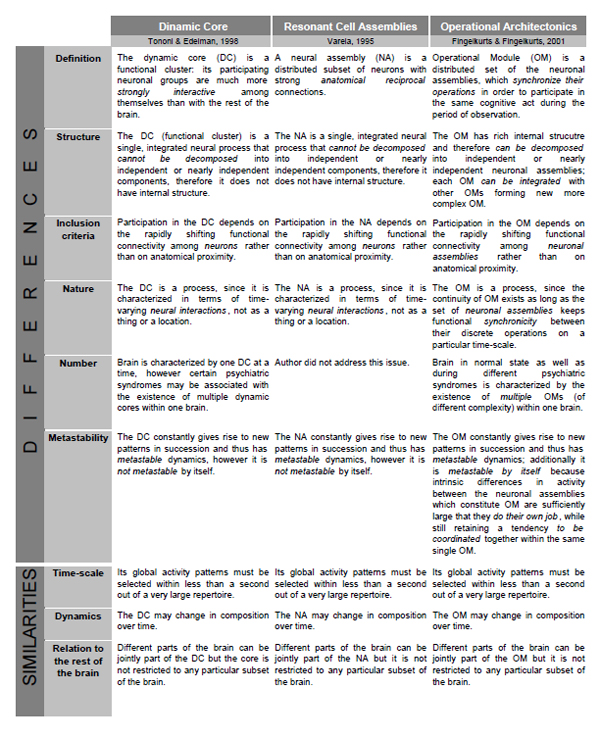 |
- Neither the Neuronal Assembly (NA) of Varela, nor the Dynamic Core (DC) of Tononi and Edelman is flexible enough to allow for a representation of complex objects or for the execution of complex combinatorial cognitive operations, which are also the gist of their internal structure. This is so because NA and DC do not have internal hierarchical organizations (structures). However, it is essentially necessary to allow for hierarchical organization with the structured integration of subcomponents [123] to represent complex phenomenal objects and operations. The components of complex objects and operations are often necessarily activated under the same overall condition; hence without defined internal structure a NA/DC could not distinguish between the two (or more) types of components or events. In contrast, Operational Modules (OMs), which are the main constituents of the OA framework, do have such internal organization [14,27,28]: one OM may be a member of another more complex one, or it may be decomposed until simple neuronal assemblies, each of which would be responsible for simple brain/cognitive operation. Therefore, the recombination of subsets of neuronal assemblies into OMs, and further of different OMs into larger structured OMs yields a vast number of potential combinations needed to represent the multivariability of cognition and eventually consciousness [7,9]. It should be stressed here that functionally, the outcome of coincident operations of many neuronal assemblies is an OM rather than larger ensemble of particular neurons firing in synchrony [14]. Such complex structure of OM can be used for semantic representations of words with similar meanings, for example, for hyponyms and hyperonyms [124]. For instance, it can be shown that between-assembly functional connections and activity dynamics are a possible basis of semantic associations and/or grammatical phenomena [124,125].
- In contrast to NA/DC models, the OA framework supposes large number of coexisting OMs. Indeed, considering the composite polyphonic character of the electrical brain field (EEG), this field may be presented as a mixture of many time-scale processes (individual frequency components) [12,99,126]. Consequently, a large amount of functionally distinct OMs can co-exist simultaneously at different time-scales and even between them [9,14,23]. Simultaneous presence of these OMs subserves the numerous operational acts on the functioning of the brain-mind and on the interaction of the organism with its environment [127]. Only subset of these OMs, however, constitutes mental states, some of which are of conscious nature (for further discussion see Ref. [9,14,27,28]).
- Even though all three theoretical frameworks stress the importance of functional connections, the concepts they use to define the values of functional connectivity differ significantly between them. This subject is discussed in a grate detail in our previous publications; therefore, we address interested reader to them [14,15]. Here we should only mention that OA framework is based on a “true” functional synchrony which does not necessarily require any anatomical connections. It is the stimulus (either external – physical or internal – phenomenological), the task, or some function that cause the synchronization; therefore, it is a function-based synchronization [14].
- The OMs in contrast to NA/DC are characterized by the metastable nature. Attention, we speak here not about dynamics of OM/NA/DC which is also metastable, but about the functional entity (OM/NA/DC) pre se. As we have already mentioned in the main body of the text, the OMs are inherently metastable since they constructed by separate neuronal assemblies. Each from these assemblies process and represent different types of information from relatively independent brain functional systems; however, at the same time these assemblies exhibit tendency for the coordinated activity [7,14,28]. Such simultaneous existence of autonomous and coordinated tendencies is the essence of the metastable regime of a brain functioning [2,3].
- NA/DC are lacking of the time-dimensional information in each cortical area separately, while the OM is based on the detailed and known time-dimensional information in each cortical area (Fig. 2). This information is presented in the sequences of concatenated quasi-stationary EEG segments (and their characteristics) revealed from the local EEG recordings [14]. The continuity of OMs exists as long as the set of TNAs keeps synchronicity between their discrete operations [28]. We argue that at the phenomenological (subjective) level during complex OM presence, a continuity of consciousness would be experienced [9,27]. This conclusion is consistent with the view presented by Damasio [128] that consciousness comes from the abundant flow of endless narratives of the processed objects and their features in different brain areas.
CONCLUSIONS
The OA theory adopts the view that brain and mental processes (a) essentially evolve over real time (a dynamical approach) and (b) are characterized by distinct microstates (a symbolic approach), which are realized by a set of distributed but functionally connected neuronal assemblies (a connectionist approach) and are the result of communication between neuronal assemblies (a computational approach). Methodologically, OA framework enables to study in a precise manner the peculiarities of transient neuronal assemblies’ behavior (local interactions in the neocortex), allowing, thus, to assess the mesolevel of brain activity description through the large-scale measures as an EEG and/or MEG.
Since it is obvious that local interactions among neurons within neuronal assemblies (mesolevel) cannot be independent from global integrative processes (macrolevel), functional interrelations between neuronal assemblies located in different cortical areas should be addressed also. With OA methodology a new type of integrative brain activity – operational synchrony – has been discovered by means of ISS measure. It is important to remind that in the case of ISS, it is not the immediate amplitudes of the EEG signals or/and their rhythmical components, but the moments of abrupt shifting of quasi-stationary EEG segments among different channels that are synchronized. This type of synchrony reflects a true functional connectivity between different brain areas by means of coupled operations (for a discussion, see Ref. [15]).
Generally, ISS (a) is a robust technique which is sensitive to temporal structure of the EEG signal; (b) accounts the nonstationary nature of this signal; (c) does not use averaging procedures and has specific tests for non-random and non-occasional nature of the results; (d) has notable topological peculiarities along the neocortex and, thus, is sensitive to morphological and functional organization of the neocortex; (e) is relatively independent on EEG spectral intensity, reference electrode and volume conduction. Together these ISS aspects lay a strong foundation for a very sensitive measure, which can be used for understanding the neural mechanisms of complex coordinated brain-mind operations within an OA framework.
ACKNOWLEDGEMENTS
The authors wish to express special gratitude for stimulating discussions on related topics to Prof. Alexander Kaplan, Prof. Walter Freeman, Prof. Erol Basar, Prof. Hermann Haken, Prof. Steve Bressler, Prof. Antti Revonsuo, Prof. Yurii Alexandrov, Prof. Ernst Pöpple, Dr. Sergei Shishkin, and Dr. Sergei Borisov. We wish also to thank all our colleagues, discussion with whom sharpened our ideas and supported our interest in the fundamental neuroscience questions. Special thanks to Carlos Neves (IT and Computer Science specialist) and Viktor Ermolaev (Dipl. Med. Eng.) for software development and technical support; and to Prof. Boris Darkhovsky for mathematical consultations. The preparation of this paper has been supported by BM-Science Centre.


