All published articles of this journal are available on ScienceDirect.
Neurally and Mathematically Motivated Architecture for Language and Thought
Abstract
Neural structures of interaction between thinking and language are unknown. This paper suggests a possible architecture motivated by neural and mathematical considerations. A mathematical requirement of computability imposes significant constraints on possible architectures consistent with brain neural structure and with a wealth of psychological knowledge. How language interacts with cognition. Do we think with words, or is thinking independent from language with words being just labels for decisions? Why is language learned by the age of 5 or 7, but acquisition of knowledge represented by learning to use this language knowledge takes a lifetime? This paper discusses hierarchical aspects of language and thought and argues that high level abstract thinking is impossible without language. We discuss a mathematical technique that can model the joint language-thought architecture, while overcoming previously encountered difficulties of computability. This architecture explains a contradiction between human ability for rational thoughtful decisions and irrationality of human thinking revealed by Tversky and Kahneman; a crucial role in this contradiction might be played by language. The proposed model resolves long-standing issues: how the brain learns correct words-object associations; why animals do not talk and think like people. We propose the role played by language emotionality in its interaction with thought. We relate the mathematical model to Humboldt’s “firmness” of languages; and discuss possible influence of language grammar on its emotionality. Psychological and brain imaging experiments related to the proposed model are discussed. Future theoretical and experimental research is outlined.
LANGUAGE AND THOUGHT
Language and thought are so closely related that it is difficult to imagine what one without the other would be. Scientific progress beginning in the 1950s toward understanding of language was based on Chomsky’s idea [1] that language is independent of thought. It explained several mysteries about language, e.g. why learning language takes few years, but learning to think takes a lifetime. Yet Chomskyan linguistics did not result in a mathematical theory. Many linguists rejected the idea of complete separation between language and cognition in Chomsky’s theories. Decades of effort by cognitive linguists and evolutionary linguists did not, however, lead to a mathematical theory unifying language and thought [2-6]. Evolutionary linguistics considered the process in which language is transferred from one generation to the next one. [7-9]. This transferring process was demonstrated to be a “bottleneck,” a process-mechanism that selected or “formed” compositional properties of language. Evolu-tionary linguistic approach demonstrated mathematically that indeed this bottleneck leads to compositional property of language. Under certain conditions a small number of sounds (phonemes, letters) are aggregated into a large number of words. Brighton et al. [10] demonstrated emergence of a compositional language due to this bottleneck mechanism. Yet, this development lacks in two fundamental aspects. First, its mathematical apparatus leads to computational difficulty (incomputable combinatorial complexity, CC), which cannot be scaled up to a realistic complexity of language. And second, objects of thoughts are supposed to be known; evolutionary linguistics has not been able so far to demonstrate how thoughts emerge in interaction with language [11].
This article aims at overcoming existing difficulties. We investigate a hypothesis of joint emergence of language and thought [11-15]. Neural mechanisms integrating language and thoughts are not known, and we concentrate on combining existing knowledge about neural brain architecture, with plausible neural hypotheses, and with mathematical models capable of overcoming CC. Existing knowledge does not allow to predict detailed neural mechanisms. Our hypotheses proposes a brain architecture. We discuss neural mechanisms necessary for supporting the proposed architecture while discovering of these mechanisms remains a challenge for future research. Our hypothesis of joint emergence of language and thought in mutual interaction relates to a growth of an individual as well as emergence of language and thought in cultural evolution. Perception of objects does not require language. This ability exists in animals lacking human language. Yet, abstract thoughts cannot emerge without language. The reason is that learning requires grounding, as it was recognized by the field of artificial intelligence a while ago. Learning without grounding could easily go wrong causing learned or invented representations to correspond to nothing real or useful [16]. The problem of grounding in learning of language and in cognition was discussed in [17-20]. At the lower levels in the hierarchy of thought learning is grounded in direct perception of the world. Learning is grounded in real objects. At higher levels, however, learning of abstract cognitive representations has no ground. Abstract thoughts are called abstract exactly for this reason, they cannot be directly perceived. Language acquisition by an individual, on the opposite, is grounded in the language, which is spoken around; this grounding exists at every level (sounds, words, syntax, phrases, etc.). There is a popular idea that abstract thoughts are learned as useful combinations of simpler objects. Mathematical analysis, however, reveals that this idea is naïve. It is mathematically impossible to learn useful combinations of objects among many more useless ones, because the number of combinations is too large. In every situation there are hundreds of objects, most of which are not relevant to this particular situation, and we learn to ignore them. Combinations of just 100 objects are 100100, an astronomical number exceeding all elementary interactions in the Universe in its entire lifetime. So, how is this learning possible? Learning which combinations are useful and which are useless is not possible during an individual lifetime. We propose a hypothesis that learning abstract ideas is only possible due to language, which accumulates millennial cultural wisdom. The speed of accumulation of knowledge in cultural evolution, likely, is combinatorially fast [21], so one CC cancels the other, which makes language emergence mathematically possible in cultural evolution. Individual language learning, as discussed, is grounded in surrounding language. We learn words, phrases, and general abstract ideas ready-made from surrounding language. Mathematical models of this process are considered in the following sections.
Thought as well as language has a hierarchical structure, illustrated in a simplified way in Fig. (1). This hierarchy is not strict, feedbacks among multiple levels play important role in language and thinking mechanisms. The fundamental aspect of these mechanisms is an interaction of bottom-up and top-down signals between adjacent levels, also called afferent and efferent signals [22]. Consider first thought and language processes separately. At every level, neural representations of concept-ideas, or internal mind models in mathematical language, project top-down signals to a lower level. Thinking or recognition processes consist in matching top-down signals to patterns in bottom-up signals coming from the lower level. A successful match results in recognition of an object, a situation, or emergence of a thought. The corresponding model is excited and sends a neural signal up the hierarchy; this is a source of bottom-up signals. At the very bottom of the hierarchy the source of bottom-up signals are sensory organs.
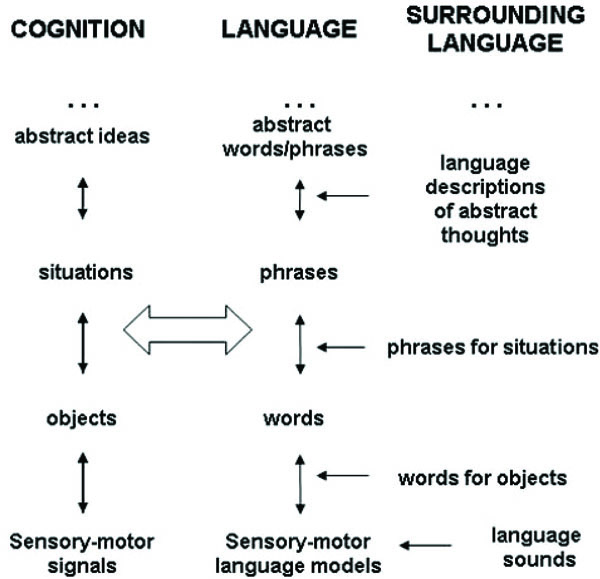
Parallel hierarchies of thought and language.
The following sections consider interacting bottom-up and top-down signals and a biological drive for this process. Then we consider mathematical models of these interactions, followed by models of interaction between thought and language.
THE KNOWLEDGE INSTINCT
Matching bottom-up and top-down signals, as mentioned, constitutes the essence of perception and cognition processes. Models stored in memory as representations of past experiences never exactly match current objects and situations. Therefore thinking and even simple perception always require modifying existing models; otherwise an organism will not be able to perceive the surroundings and will not be able to survive. Therefore humans and higher animals have an inborn drive to fit top-down and bottom-up signals. We call this mechanism the knowledge instinct, KI [13,23-25]. This mechanism is similar to other instincts [13, 26]) in that our mind has a sensor-like mechanism that measures a similarity between top-down and bottom-up signals, between concept-models and sensory percepts. Brain areas participating in the knowledge instinct were discussed in [27]. As discussed in that publication, biologists considered similar mechanisms since the 1950s; without a mathematical formulation, however, its fundamental role in cognition was difficult to discern. All learning algorithms have some models of this instinct, maximizing correspondence between sensory input and an algorithm internal structure (knowledge in a wide sense). According to [26] instinct-emotion theory, satisfaction or dissatisfaction of every instinct is communicated to other brain areas by emotional neural signals. We feel these emotional signals as harmony or disharmony between our knowledge-models and the world. At lower levels of everyday object recognition these emotions are usually below the threshold of consciousness; at higher levels of abstract and general concepts this feeling of harmony or disharmony could be strong, as discussed in [13,28] it is a foundation of human higher mental abilities.
Mathematical models of matching bottom-up and top-down signals have been developed for decades. This development met with mathematical difficulty of CC. This CC is related to the fact that in every concrete situation objects are encountered in different color, angle, lighting…, but in addition, objects are encountered in different combinations. As discussed, every situation is a collection of many objects. Most of them are irrelevant to recognition of this situation and separating relevant from irrelevant objects leads to CC. The same is true about language. Every phrase is a collection of words, and only some of these words are essential for understanding the phrase. This problem is even more complex for understanding paragraphs or larger chunks of texts. Learning language also requires overcoming CC. Mathematically, CC is related to formal logic, which turned out to be used by most mathematical procedures, even by those specifically designed to overcome logic limitations, such as neural networks and fuzzy logic [25,29-31,64]. The mathematics capable of overcoming CC, dynamic logic (DL), which models the process of satisfaction of KI, while overcoming CC has been developed in [13,23-25,32-34]. In several cases it was mathematically proved that DL achieves the best possible performance [35-38]. The next section describes extension of DL applicable to the hierarchical architectures. Here we discuss DL conceptually.
The fundamental property of DL, which enables it to overcome CC, is a process “from vague-to-crisp” [25, 30,31]. In this process vague representations-models evolve into crisp ones, matching patterns in bottom-up signals without CC. The DL process mathematically models actual neural processes in the brain. This can be illustrated, based on current knowledge of the brain neural architecture, with a simple experiment. Just close your eyes and imagine an object in front of you. The imagined object is vague-fuzzy, not as crisp as a perception with opened eyes. We know that this imagination is a top-down projection of models-representations onto the visual cortex. This demonstrates that models-representations are vague, similar to models in the initial state of the DL process. When you open your eyes, these vague models interact with bottom-up signals projected onto the visual cortex from retinas. In this interaction vague models turn into crisp perceptions as in the DL process. Note, that with opened eyes it is virtually impossible to recollect vague images perceived with closed eyes; during usual perception with opened eyes, we are unconscious about the DL-process from vague to crisp. It is our hypothesis that vague representations are virtually inaccessible to consciousness; this hypothesis is similar to Grossberg’s [22] suggestion that only representations matching bottom-up signals in the state of resonance are accessible to consciousness.
Similar experiments were conducted in much more details using neuro-imaging technology [39]. They confirmed that the initial state of representations is vague. The process from vague-to-crisp, in which vague models match patterns in retinal signals takes about 160 ms. This process is unconscious. Only the final state of the process, a crisp perception of an object is conscious. Authors also identified brain modules participating in this perception process.
It is our hypothesis that not only perception, but all thought processes at all levels in the hierarchy proceed according to DL, the process from vague-to-crisp. These are processes, in which new thoughts are born, when vague thoughts-representations, results of previous thought processes, interact with current reality. These processes of creating new thoughts are driven by an inborn mechanism, a striving to match thoughts to reality. This mechanism has been called a need for knowledge, curiosity, cognitive dissonance, or KI [25,40-42]. Mathematical modeling of perception and thinking revealed fundamental nature of this instinct: all mathematical algorithms for learning have some variation of this process, matching bottom-up and top-down signals. Without matching previous models to the current reality we will not perceive objects, or abstract ideas, or make plans. This process involves learning-related emotions evaluating satisfaction of KI [25,26,28,43].
Bar et al. [39] demonstrated neural mechanisms of DL in visual perception. Demonstrating neural mechanisms of DL for higher cognitive levels, for language, and for joint operations of learning and cognition is a challenge for future research and we hope that mathematical theory proposed in this paper will help identifying experimental approaches.
This process of creating new knowledge however is not the only way of decision making. Most of the time, most people do not use KI and do not create new knowledge corresponding to their circumstances. More often people rely on ready-made rules, heuristics, even if they only approximately correspond to concrete individual situations. This preference for rules, heuristics, instead of original thinking is the content of Tversky and Kahneman [44,45] theory that received Nobel Prize in 2002. This reliance on heuristics, even in cases when correct decisions are easily within grasp of one’s thinking, psychologists often call basic irrationality of human thought [27,46]. After discussing the DL model of combining language and thinking driven by KI, we discuss a possible role of language in thinking according to irrational heuristics.
DYNAMIC LOGIC
Mathematical Formulation
We summarize now a mathematical theory combining the discussed mechanisms of language and thinking as interaction between top-down and bottom-up signals at a single layer in multi-layer hierarchical system following [13,47,48]. Although language and cognition are not strict hierarchies and interactions across several hierarchical levels are present, for simplicity we will use the word hierarchy. The knowledge instinct maximizes a similarity measure L between top-down signals M and bottom-up signals X,
Here curved brackets indicate that there are sets of top-down and bottom-up signals; l(n|m) is a shortened notation for l(Xn|Mm), a partial similarity of a bottom-up signal in pixel n given that it originated from model h. Similarity L accounts for all combinations of signals n coming from any model m, hence the huge number of items MN in eq.(1); this is a basic reason for CC of most algorithms. Models depend on unknown parameter values S, Mm(S).
The learning instinct demands maximizing the similarity L over model parameters S. Dynamic logic maximizes similarity L while matching vagueness or fuzziness of similarity measures to the uncertainty of models. It starts with any unknown values of parameters S and defines association variables f(m|n)
Initially, parameter values are not known, and uncertainty of partial similarities is high. So the fuzziness of the association variables is high. In the process of learning, models become more accurate, and association variables more crisp, as the value of the similarity increases. Dynamic logic process always converges as proven in [25].
Earlier formulations of using dynamic logic for learning language were considered in [49-52]. Here we consider a more powerful model. We consider a model of interaction between two adjacent levels. For concreteness, we discuss a child learning to recognize situations (upper level), assuming that objects constituting situations (lower level) are known. This is a simplification, in real life multiple hierarchical levels are learned in parallel We use this simplification for an ease of presentation, it is not essential for the mathematical method. For the hierarchical system of cognition or language the partial similarities are defined according to [48] using binomial distribution,
Here, Do is the total number of objects that the child can recognize; n is the index of an observed situation encountered by the child; m is the index of a model (of a state in the child’s brain); and i is the index of an object; pmi are model parameters, they are probabilities that object i is present in situation-model m; xni are data indicating presence (x=1) or absence (x=0) of object i in observed situation n. In every situation the child perceives Dp objects. This is a much smaller number compared to Do. Each situation is also characterized by the presence of Ds objects essential for this situation (Ds < Dp). Normally nonessential objects are present and Ds is therefore less than Dp. There are situations important for learning (Ds>0) and many clutter situations, composed of random collections of objects, which the child should learn to ignore.
The DL process is an iterative estimation of the model parameters, pmi. First it starts with all probabilities set randomly within a narrow range around 0.5; this corresponds to a vague initial state, in which all objects have approximately equal probabilities of belonging to any situation-model. The iterative DL process is defined as follows. Second, association variables f(m|n) are defined according to (2). Third, parameter values are updated according to ([47])
An intuitive meaning of this equation is that probabilities are weighted averages of the data. Upon convergence, associations f(m|n) converge to 0 or 1, and probabilities for each situation are average values of data for this situation. The DL iterations are defined by repeating the second and third steps until convergence, which is illustrated below.
Simulation Examples
We set the total number of objects to Do=100; the number of objects observed in a situation Dp = 10; in situations important for learning there are 5 objects characteristical of this situation, Ds = 5; in clutter situations, Ds = 0. There are total of 10 important situations, each is simulated 25 times; in each simulation Ds = 5 characteristic objects are repeated and the other 5 selected randomly. This yields total of 250 situations. We also generated 250 clutter situations, in which all objects are randomly selected. This data is illustrated in Fig. (2). The objects present in a situation (x=1) are shown in white and absent, x=0, are shown in black. In this figure objects are along the vertical axes and situations are along the horizontal axes; situations are sorted, so that the same situations are repeated. This results in horizontal white lines for characteristic objects for the first 10 situations.

The objects present in a situation (x=1) are shown in white and absent objects (x=0) are shown in black. In this figure objects are along the vertical axes and situations are along the horizontal axes; situations are sorted, so that the same situations are repeated. This results in horizontal white lines for characteristic objects for the first 10 situations (each repeated 25 times).
In real life situations are not encountered sorted. A more realistic situation is shown in Fig. (3), in which the same data are shown with situations occurring randomly.

Same data as in Fig. (2, with situations occurring randomly).
The DL iterations are initiated as described in the previous section. The number of model is unknown and was set arbitrarily to 20. It is possible to modify DL iterations so that situations are initiated as needed but it would be difficult to present such results in the paper. Even so the total number of models was set incorrectly, DL converged fast, with 10 models converging to the important models and the rest converging to clutter models. The convergence results are shown in Fig. (4), illustrating the initial vague models and their changes at iterations 1, 2, and 10.
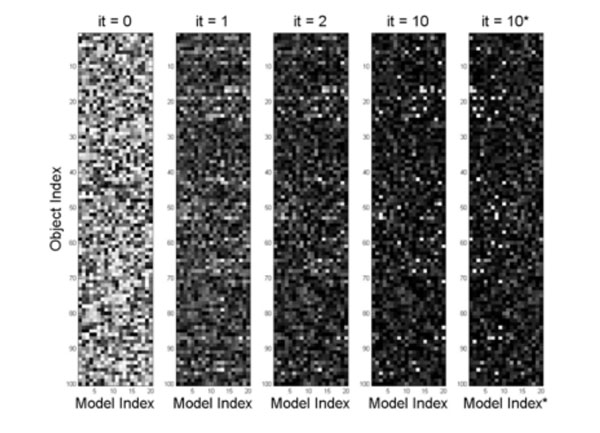
The convergence results are shown in 5 columns; the first one illustrates the initial vague models and the following show model changes at iterations it = 1, 2, and 10. Each column here illustrates all 20 models, along the horizontal axes, and objects are shown along the vertical axes as in previous figures. The last column (10*) shows iteration 10 sorted along the horizontal axes, so that the 10 models most similar to the true ones are shown first. One can see that the left part of the figure contains models with bright pixels (characteristic objects) and the right part of the figure is dark (clutter models).
Each column here illustrates all 20 models, along the horizontal axes, and objects are shown along the vertical axes as in previous figures. The last column (10*) shows iteration 10 resorted along the horizontal axes, so that the 10 models most similar to the true ones are shown first. One can see that the left part of the figure contains models with bright pixels (characteristic objects) and the right part of the figure is dark (clutter models). In the next section we illustrate this fast convergence numerically, along with studying the language effect.
Effect of Language
In the above simulations, if objects are substituted with words and situations with phrases, the result will be learning which phrases are typical in this language. Also, we did not consider relations among objects specifically; nevertheless our DL formalization does not exclude relations from a list of objects. A complete consideration in future will include relations and markers, indicating which objects and in which way are related; these relations, markers and their learning are not different mathematically from objects. In case of language, relations and markers would address syntax.
The next step would be joint learning of language and cognition, and demonstrating that such learning is more powerful than cognitive learning alone. A step toward joint language and cognition learning could be to repeat the above learning cases in a cross-situational learning; that is when phrases corresponding to situations are presented along with multiple situations, as in real life, so that correspondences among words-phrases and objects-situations are uncertain and have to be learned. This project will be presented in the following publication. Here we study a first step toward this goal of combining language and cognition. When presenting situations for learning, one of the important situations (among 25 repetitions) is presented with a word-label for this situation. As expected, this leads to better learning illustrated in Fig. (5). In this figure lines with black dots illustrate performance of the case considered in the previous section without language effects. Convergence is measured using the total similarity between the data and models (lower part of the figure) and using errors between the model probability and data (the upper part of the figure; for every situation the best matching model is selected). Lines with open circle indicate performance with language supervision: for each situation, 1 of the 25 simulations came with a word-label, so that important situations were easier to separate from one another and from random clutter situations.
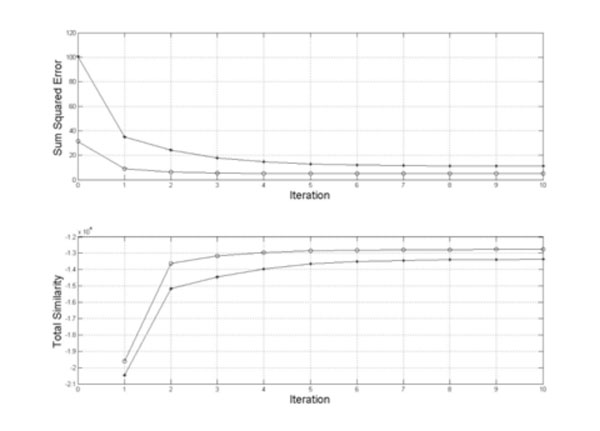
Lines with black dots illustrate performance of the case considered in the previous section without language effects. Convergence is measured using the total similarity between the data and models (lower part of the figure) and using errors between the model probability and data (the upper part of the figure; for every situation the best matching model is selected). Lines with open circle indicate performance with language supervision. In each case convergence is attained within few iterations, and language supervision improved performance, as expected.
JOINT LANGUAGE AND THOUGHT
DL described in the previous section has overcome CC of learning situations and phrases. The simulation examples illustrated fast convergence. However the problem of joint learning of language and though was not addressed. This would require architecture capable of learning two parallel hierarchies of Fig. (1) for two cases, first, individual learning from surrounding language, and second, emergence of language and thought in cultural evolution.
We propose a hypothesis that integration of language and cognition is accomplished by a dual model. Every model in the human brain is not separately cognitive or linguistic, and still cognitive and linguistic contents are separate to a significant extent. Every concept-model Mm has two parts, linguistic MLm and cognitive MCm:
This dual-model equation suggests that connection between language and cognitive models is inborn. In a newborn mind both types of models are vague mostly empty placeholders for future cognitive and language contents. An image, say of a chair, and sound “chair” do not exist in a newborn mind. Mathematically this corresponds to probabilities, pCmi and pLmi, being near 0.5, so that every visual or hearing perception has a probability of belonging to every concept (object, situation, etc.). But the neural connections between the two types of models are inborn; the brain does not have to learn which concrete word goes with which concrete object. Future simulations would demonstrate that as models acquire specific contents in the process of growing up and learning, linguistic and cognitive contents are always staying properly connected. While babies learn language models at the level of objects or situations, the corresponding models become crisper and less vague (the corresponding probabilities, pCmi and pLmi, become closer to 0 or 1).
Language models become less vague and more specific much faster than the corresponding cognitive models for the reason that they are acquired ready-made from surrounding language. This is especially true about contents of abstract models, which cannot be directly perceived by the senses, such as “law,” “abstractness,” “rationality.” This explains how it is possible that kids by the age of five can talk about most of contents of the surrounding culture but cannot function like adults: language models are acquired ready-made from the surrounding language, but cognitive models remain vague and gradually acquire concrete contents throughout life. According to the dual-model hypothesis, this is an important aspect of the mechanism of what is colloquially called “acquiring experience.” It would be important in future research first, to identify detailed neural mechanisms of models, second, the neural mechanism of connections between language and cognitive models, and third, to correlate the suggested mechanism (of cognitive models becoming crisper) with currently known maturation mechanism of myelination, reaching into adulthood. Here we emphasize what could the reason be for significant differences in speeds of learning language and cognitive models.
This dual-model hypothesis also suggests that the inborn neural connection between cognitive brain modules and language brain modules (evolving over thousands or millions of years of evolution) is sufficient to set humans on an evolutionary path separating us from animal kingdom.
Human learning of cognitive models continues through the lifetime and is guided by language models. Here we would like to remind the experiment with closed eyes described in section 1. It is virtually impossible to remember imagined perceptions when eyes are opened. Similarly, language plays a role of eyes for abstract thoughts. On one hand, abstract thoughts are only possible due to language, on the other, language “blinds” our mind to vagueness of abstract thoughts. Whenever one can talk about an abstract topic, he (or she) might think that the thought is clear and conscious in his mind. But the above discussion suggests that we are conscious about language models of the dual hierarchy. Cognitive models in most cases may remain vague and unconscious. The higher up in the hierarchy the vaguer are contents of abstract thoughts, while due to crispness of language models we may remain convinced of clear conscious thoughts.
We suggest that basic human irrationality (which discovery was initiated in works of Tversky and Kahneman [44,45]; leading to 2002 Nobel Prize), discussed in section 1, originates from this dichotomy between cognition and language. Language is significantly crisp in the human brain, while cognition might be vague. Using the KI mechanisms to arrive at rational decisions (to make cognitive models crisp) requires special effort and training. Language accumulates millennial cultural wisdom and it might be to one’s advantage to rely on heuristics formulated in language. This suggestion is a scientific hypothesis that can be and should be verified experimentally. In this future verification it is necessary to carefully consider the role of emotions. It was suggested that irrational heuristic decision making vs. KI-deliberate analysis activates amygdala stronger than the cortex [27]. So that emotions may play a larger role in irrational decision making. Two words of caution are due. First, emotional decision making could be perfectly rational [53] and not necessarily related preferentially to amygdala). Second, these rational emotions might be different from specific language emotions considered in the next section.
LANGUAGE EMOTIONALITY, OR EMOTIONAL SAPIR-WHORF HYPOTHESIS
The knowledge instinct drives the human brain to develop more specific, concrete and conscious cognitive models by accumulating experience throughout life in correspondence with language models. For this process to remain active brains have to maintain “motivation” to do it. This motivation is not automatic. We suggest a hypothesis that there are specific emotions related to language [54]. Origin of language required freeing vocalization from uncontrolled emotional influences. Initial undifferentiated unity of emotional, conceptual, and behavioral-(including voicing) mechanisms had to separate-differentiate into partially independent systems. Voicing separated from emotional control due to a separate emotional center in cortex which controls larynx muscles, and which is partially under volitional control [55,56]. Evolution of this volitional emotional mechanism possibly paralleled evolution of language computational mechanisms. In contemporary languages the conceptual and emotional mechanisms are significantly differentiated, as compared to animal vocalizations. The languages evolved toward conceptual contents, while their emotional contents were reduced. Cognition, or understanding of the world, is due to mechanisms of concepts, which we refer to as internal representations or models. Barsalou calls this mechanism situated simulation [57].
Language and voice started separating from ancient emotional centers possibly millions of years ago. Nevertheless, emotions are present in contemporary languages [54]. Emotionality of languages is carried in language sounds, what linguists call prosody or melody of speech. Emotions in language sounds may affect ancient emotional centers of the brain. This ability of human voice to affect us emotionally is most pronounced in songs. Songs and music, however, is a separate topic [58,59] not addressed in this paper.
Everyday speech is low in emotions, unless affectivity is specifically intended. We may not notice emotionality of everyday “non-affective” speech. Nevertheless, “the right level” of emotionality is crucial for developing cognitive parts of models. If language parts of models were highly emotional, any discourse would immediately resort to blows and there would be no room for language development (as among primates). If language parts of models were non-emotional at all, there would be no motivational force to engage into conversations, to develop cognitive models. The motivation for developing higher cognitive models would possibly be reduced. Lower cognitive models, say for object perception, would be developed because they are imperative for survival and because they can be developed independently from language, based on direct sensory perceptions, like in animals. But models of situations and higher cognition, as we discussed) are developed based on language models. As discussed later, this requires emotional connections between cognitive and language models.
Primordial fused language-cognition-emotional models, as discussed, have differentiated long ago. The involuntary connections between voice-emotion-cognition have dissolved with emergence of language. They have been replaced with habitual connections. Sounds of all languages have changed and, it seems, sound-emotion-meaning connections in languages should have severed. Nevertheless, if the sounds of a language change slowly, connections between sounds and meanings persist and consequently the emotion-meaning connections persist. This persistence is a foundation of meanings because meanings imply motivations. If the sounds of a language change too fast, the cognitive models are severed from motivations, and meanings disappear. If the sounds change too slowly the meanings are nailed emotionally to the old ways, and culture stagnates.
This statement is a controversial issue, and indeed, it may sound puzzling. Doesn’t culture direct language changes or is the language the driving force of cultural evolution? Direct experimental evidence is limited; it will have to be addressed by future research. Theoretical considerations suggest no neural or mathematical mechanism for culture directing evolution of language through generations; just the opposite, most of cultural contents are transmitted through language. Cognitive models contain cultural meanings separate from language [11], but transmission of cognitive models from generation to generation is mostly facilitated by language. Cultural habits and visual arts can preserve and transfer meanings, but they contain a minor part of cultural wisdom and meanings comparative to those transmitted through the language. Language models are major containers of cultural knowledge shared among individual minds and collective culture.
The arguments in the previous two paragraphs suggest that an important step toward understanding cultural evolution is to identify mechanisms determining changes of the language sounds. As discussed below, changes in the language sounds are controlled by grammar. In inflectional languages, affixes, endings, and other inflectional devices are fused with sounds of word roots. Pronunciation-sounds of affixes are controlled by few rules, which persist over thousands of words. These few rules are manifest in every phrase. Therefore every child learns to pronounce them correctly. Positions of vocal tract and mouth muscles for pronunciation of affixes (etc.) are fixed throughout population and are conserved throughout generations. Correspondingly, pronunciation of whole words cannot vary too much, and language sound changes slowly. Inflections therefore play a role of “tail that wags the dog” as they anchor language sounds and preserve meanings. This, we suggest is what Humboldt [66] meant by “firmness” of inflectional languages. When inflections disappear, this anchor is no more and nothing prevents the sounds of language to become fluid and change with every generation.
This has happened with English language after transition from Middle English to Modern English [67], most of inflections have disappeared and sound of the language started changing within each generation with this process continuing today. English evolved into a powerful tool of cognition unencumbered by excessive emotionality. English language spreads democracy, science, and technology around the world. This has been made possible by conceptual differentiation empowered by language, which overtook emotional synthesis. But the loss of synthesis has also lead to ambiguity of meanings and values. Current English language cultures face internal crises, uncertainty about meanings and purposes. Many people cannot cope with diversity of life. Future research in psycholinguistics, anthropology, history, historical and comparative linguistics, and cultural studies will examine interactions between languages and cultures. Initial experimental evidence suggests emotional differences among languages consistent with our hypothesis[68,69].
Neural mechanisms of grammar, language sound, related emotions-motivations, and meanings hold a key to connecting neural mechanisms in the individual brains to evolution of cultures. Studying them experimentally is a challenge for future research. It is not even so much a challenge, because experimental methodologies are at hand; they just should be applied to these issues, and several research groups pursue these experiments.
DISCUSSION AND FUTURE DIRECTIONS
In this paper we developed mathematical architecture based on DL for joint language and cognition. This includes parallel hierarchies, dual model, similarity measures suitable for every level in the hierarchy. Algorithms used in the past for selecting subsets according to a criterion, had to resort to sorting through combinations, and faced an impenetrable wall of CC. The proposed mathematics of DL is a fundamental development overcoming this CC difficulty encountered for decades.
This development is based on known brain mechanisms, and as discussed, is partially supported by neural evidence. The neural evidence for the basic mechanism of DL, a process from vague to crisp, was demonstrated in visual perception by Bar et al. ([39]). Experimental neural evidence for other proposed models, for the parallel hierarchies, the dual model, the role of emotions, as mentioned, is in the incipient stage. Neural mechanisms predicted by our mathematical formulation include similar mechanism for higher cognitive models, as well as for language models. Below we speculate about more specific neural predictions, but we would emphasize that we welcome neuroscientists for joint discussions of what is likely and what is possible.
We predict mathematically-specific interactions in eq. (3) between bottom-up signals (xni) and model parameters (pmi). Collections of these model parameters constitute the model-representation. How numerical values of these model parameters (between 0 and 1) are neurally represented? We predict that in the initial not-learned model state parameter values are about 0.5 (“vague”); how this “non-committed” state is represented neurally? It could be due to synapse values or due to randomness of timing of arriving signals. The model learning consists in establishing which parameters of the model reach low or high values (0 or 1) for the model to be excited. According to the standard neuronal model, the concept-representation-model can be realized by one neuron with excitatory and inhibitory synapses. This model-neuron is excited when a significant number of its excitatory synapses receive signals, while inhibitory synapses don’t. Learning consists in modification-selection of excitatory and inhibitory synapses. Maturation might consist in reducing the number of modifiable synapses (synapses corresponding to many black dots in Fig. 4 would die out, leaving only few to ensure some minimal adaptivity). This description constitutes a hypothesis about neural realization of eq.(3). We would be looking forward to discussing with neural scientists, which other realization might be possible and testable. Eq. (2) is a standard competitive neural organization, which implements competitions among models with input signals from eq.(3) models, which compete through feedback connections.
The dual model in particular proposes a testable neural prediction, neural connections between cognitive and language models. Quite possible that in neural terms this means myelination of fibers. The first experimental indication of neural mechanisms for the dual model has appeared in [65]. Those researchers demonstrated that categorical perception of color in prelinguistic infants is based in the right brain hemisphere. As language is acquired and access to lexical color codes becomes more automatic, categorical perception of color moves to the left hemisphere (between two and five years) and adult’s categorical perception of color is based in the left hemisphere (where language mechanisms are located).
This fast brain rewiring might be due to a different mechanism than learning cognitive categories, it looks like the opposite mechanism: cognition is blocked by language. In any case this provides evidence for neural connections between perception and language, a foundation of the dual model. Possibly it confirms that aspect of the dual model: the crisp and conscious language part of the model hides from our consciousness vaguer cognitive part of the model. This is similar to what we observed in the closed-open eye experiment: with opened eyes we are not conscious about vague imaginations-priming signals. Still, direct neural evidence for the dual model is for future research.
This paper suggest a hypotheses to answer some mysteries of language and its interaction with thought posed at the beginning. Language and thought are separate and closely related mechanisms of the mind. They evolve jointly in ontological development, learning, and possibly these abilities evolved jointly in evolution. This joint evolution of dual models from vague to more crisp content resolves the puzzle of associationism: there is no need to learn correct associations among combinatorially large number of possible associations, words and objects are associated all the time while their concrete contents emerge in the brain.
Even simple perception of objects that can be directly perceived by sensing according to the referenced experimental data, is affected by language. In more complex cognition of abstract ideas, which cannot be directly perceived by the senses, we conclude that language parts of models are more crisp and conscious; language models guide the development of the content of cognitive models. Language models also tend to hide cognitive contents from consciousness. It follows that in everyday life most thinking is accomplished by using language models, possibly with little engagement of cognitive contents. Possibly fusiform gyrus plays a role in cognition shadowed by language. More detailed discussion of possible brain regions involved in the knowledge instinct are discussed in [27]. This is a vast field for experimental psychological and neuro-imaging investigations.
The proposed models bear on fundamental discussions in psycholinguistics. Hauser, Chomsky, and Fitch [60] emphasized that “language is, fundamentally, a system of sound-meaning connections.” This connection is accomplished by a language faculty, which generates internal representations and maps them into the sensory-motor interface, and into the conceptual-intentional interface. In this way sound and meaning are connected. They emphasized that the most important property of this mechanism is recursion. However, they did not propose specific mechanisms how recursion creates representations, nor how it maps representations into the sensory-motor or conceptual-intentional interfaces.
The current paper suggests that it might not be necessary to postulate recursion as a fundamental property of a language faculty. In terms of the mathematical model proposed here, recursion is accomplished by the hierarchy: a higher layer generates lower layer models, which accomplish recursive functions. We have demonstrated that the dual model is a necessary condition for the hierarchy of cognitive representations. It also might be a sufficient one. It is expected that the hierarchy is not a separate inborn mechanism; the hierarchy might emerge in operations of the dual model and dynamic logic in a society of interacting agents with intergenerational communications (along the lines of Brighton et al. [61]). What exactly are the inborn precursors necessary for the hierarchy’s ontological emergence, if any, is a challenge for the ongoing research. Anyway, reformulating the property of recursion in terms of a hierarchy, along with demonstrating that a hierarchy requires the dual model, the paper has suggested a new explanation that a single neurally-simple mechanism is unique for human language and cognitive abilities. Initial experimental evidence indicates a support for the dual model; still further experiments elucidating properties of the dual model are needed.
This paper also suggests that the mechanism of mapping between linguistic and cognitive representations is accomplished by the dual models. In previous sections we considered mathematical modeling of the “conceptual-intentional interface” for intentionality given by the knowledge and language instincts; in other words we considered only intentionalities related to language and knowledge. It would not be principally difficult to add other types of intentional drives following [26]. The current paper has not considered the “sensory-motor interface,” which of course is essential for language production and hearing. This can be accomplished by the same mechanism of the dual model, with addition of behavioral and sensorial models. This task is not trivial; still it does not present principal mathematical difficulties.
We would also like to challenge an established view that specific vocalization is “arbitrary in terms of its association with a particular context.” In animals, voice directly affects ancient emotional centers of the brain. In humans these affects are obvious in songs, still persist in language to certain extent. It follows that sound-intentional interface is different from language-cognition interface modeled by the dual model. The dual model frees language from emotional encumbrances and enables abstract cognitive development to some extent independent from primitive ancient emotions. Arbitrariness of vocalization (even to some extent) could only be a result of long evolution of vocalizations from primordial sounds [62]. Understanding evolutionary separation of cognition from direct emotional-motivational control from immediate behavioral connections are other challenges for future research, and we suggest that the remaining emotional connections are fundamental for continued cultural evolution.
The proposed architecture for language-thought interaction bears on several aspects of a long standing debate about the nature of representations of symbols in human symbolic thought (see [57]; and discussions therein). Specific discussion poles centered on perceptual vs. amodal symbols with distinguished scientific schools on each side. The dual model suggests that structure of cognitive models may implement the Barsalou outline for perceptual symbols; and their learning mechanism follows the procedure of section 3. The other side of human thinking, usually associated with amodal symbols, is represented to significant extent in language models.
Language is closer to logical thinking than cognitive mechanisms proposed here. Is language an amodal symbol system? To answer this question let us look into evolution of language from animal vocalizations [12, 13,59]. Animal vocalizations are much less differentiated than humans’; conceptual, emotional, and behavioral contents are not separated, they are unified. Vocalizations are not as voluntary (if at all) as humans’. Evolution of language required separation of conceptual, semantic contents from emotional ones, and from involuntary vocalizations.
Language evolution reduces its original emotionality and acquires an ability to approximate an amodal symbol system. This ability is important for evolution of high culture, science, technology. However, an amodal symbol system is not an “ideal” evolutionary goal of language. To have meaning, to support cognition, language must be unified with cognition into the dual hierarchy. As discussed, this involves the knowledge instinct and aesthetic emotions. Language without emotionality loses this ability to unify with cognition. Amodal symbols are logical constructs, and as we discussed throughout the paper, logic is not a fundamental mind mechanism, but is only a final result of dynamic logic, and likely involves only a tiny part of the mind operations.
While language was evolving to less emotional, more semantic ability that differentiated psyche, another part of primordial vocalization was evolving toward more emotional, less semantic ability that maintained a unity of psyche. This ability evolved into music [58]. Cultures with semantically rich languages also evolved emotionally rich music [59,62]. Songs affect us by unifying semantic contents of lyrics with emotional contents of sounds, which are perceived by ancient emotional brain centers. The same mechanism still exists to a lesser degree in languages; all existing languages retain some degree of emotionality in their sounds.
Existence of sign languages poses a separate set of questions not addressed here: how emotions are carried in sign languages? Do people without hearing face specific developmental problems related to language emotions? What science can suggest mitigating these problems?
Languages, while evolving amodal symbol abilities, still retain their vocal modalities, and otherwise they will not be able to support the process of cognitive and cultural evolution. Symbolic structures of the mind are mathematically described by dynamic logic; the mind symbols are not static categories, but the dynamic logic processes. Due to the dual model they combine cognition and language, and can approximate amodal properties. The dual model suggests experimentally testable neural mechanisms—neural connections—combining two modal (perceptual, voice) symbol systems with the amodal ability.
The dual model mechanism proposes a relatively minimal neural change from the animal to the human mind. Possibly it has emerged through combined cultural and genetic evolution and this cultural evolution most likely continues today. Dynamic logic resolves a long-standing mystery of how human language, thinking, and culture could have evolved in a seemingly single big step, too large for an evolutionary mutation, too fast and involving too many advances in language, thinking, and culture, happening almost momentarily around 50,000 years ago [55,56]. Dynamic logic along with the dual model explains how changes, which seem to involve improbable steps according to logical intuition, actually occur through continuous dynamics. The proposed theory provides a mathematical basis for concurrent emergence of hierarchical human language and cognition. The dual model is directly testable experimentally. Next steps would further develop this theory in multi-agent simulations, leading to more specific and experimentally testable predictions.
The proposed theory provides solutions to classical problems of conceptual relations, binding, and recursion through the mechanisms of the hierarchy; in addition it explains how language acquires meanings in connecting with cognition due to the mechanism of the dual model. The proposed solutions overcame combinatorial complexity of classical methods, the fundamental reason for their failures despite decades of development. Predictions in this paper are experimentally testable and several groups of psychologists and neuroscientists are working in these directions.
Evolutionary linguistics and cognitive science have to face a challenge of studying and documenting how primordial fused model differentiated into several significantly-independent mechanisms. In animal minds emotion-motivation, conceptual understanding, and behavior-voicing have been undifferentiated unity, their differentiation is a hallmark of human evolution. Was this a single step, or could evolutionary anthropology document several steps, when different parts of the model differentiated from the primordial whole?
Future mathematical and experimental development should address ontological emergence of the hierarchy. Our mathematical model predicts a hierarchy of integrated language and cognitive models. Finding detailed neural mechanisms of the models, of the hierarchy, and neuronal connections corresponding to the dual model is a challenge for future experimental neural research. Lower hierarchical levels, below words and objects, should be developed theoretically, or better to say, dynamic logic should be integrated with ongoing development in this area (see [63]). Mathematical simulations of the proposed mechanisms should be extended to engineering developments of Internet search engines with elements of language understanding. The next step would be developing interactive environments, where computers will interact among themselves and with people, gradually evolving human language and cognitive abilities. Developing intelligent computers and understanding the mind would continue to enrich each other.
We emphasize that the proposed approach of dynamic logic, the dual model, and parallel hierarchies is a step toward unification of basic approaches to knowledge, its evolution, and learning in modern cognitive and neural sciences. These addresses classic representational approaches based on logic, rule systems, and amodal symbols; statistical pattern recognition and learning; embodied approaches of classic empiricism, situated actions, and cognitive linguistics; evolutionary linguistics; connectionism and neural networks. This step toward unification outlines a wide field for future theoretical and experimental research.
ACKNOWLEDGMENTS
The authors would like to thank M. Bar, R. Brockett, R. Deming, J. Gleason, D. Levine, R. Linnehan, R. Kozma, and B. Weijers for discussions, help, and advice. We are also thankful to an anonymous reviewer for valuable suggestions. This work was supported in part by AFOSR under the Laboratory Task 05SN02COR, PM Dr. Jon Sjogren, by Laboratory Task 08RY02COR, PM Dr. Doug Cochran and by NRC fellowship.


