All published articles of this journal are available on ScienceDirect.
High-Frequency Time-Resolved Scanning Acoustic Microscopy for Biomedical Applications
Abstract
High-frequency focused ultrasound has emerged as a powerful modality for both biomedical imaging and elastography. It is gaining more attention due to its capability to outperform many other imaging modalities at a submicron resolution. Besides imaging, high-frequency ultrasound or acoustic biomicroscopy has been used in a wide range of applications to assess the elastic and mechanical properties at the tissue and single cell level. The interest in acoustic microscopy stems from the awareness of the relationship between biomechanical and the underlying biochemical processes in cells and the vast impact these interactions have on the onset and progression of disease. Furthermore, ultrasound biomicroscopy is characterized by its non-invasive and non-destructive approach. This, in turn, allows for spatiotemporal studies of dynamic processes without the employment of histochemistry that can compromise the integrity of the samples. Numerous techniques have been developed in the field of acoustic microscopy. This review paper discusses high-frequency ultrasound theory and applications for both imaging and elastography.
1. INTRODUCTION
Biomechanical factors play a crucial role in regulating cell physiology, including cell division, cell locomotion, and cell adhesion [1-4]. There is an intricate relationship between single-cell biomechanics and the onset and progression of disease [2, 5-7]. During cancer metastasis, for example, cells undergo elastic deformations to intra- and extravasate through the endothelial lining of blood vessels toward the formation of secondary tumors [6, 8-10]. Despite significant advances in the field, the mechanical properties pertinent to deformation mechanisms of cancerous cells remain primarily elusive [5, 11]. Malignant cells typically respond as either less elastic (softer) or less viscous (less resistant to flow) to external stress exerted onto them from their immediate microenvironment [6, 11].
Numerous techniques have been developed for studying the mechanical and elastic properties of cells and tissues [6, 12] including: (i) micropipette technique [4, 13]; (ii) magnetic twisting cytometry [14, 15]; (iii) optical tweezers, laser tweezers or optical clamps [16, 17]; (iv) optical stretcher [18, 19], and (v) atomic force microscopy [20, 21].
The primary challenge in measuring viscoelastic properties not only of cancer cells but of any other cell type lies in the fact that physiological conditions resembling their native environment should be maintained. In general, viscoelastic cell properties are dependent on external stimuli [22, 23].
Scanning Acoustic Microscopy (SAM) is a robust approach for the study of viscoelastic properties of biological tissues and single cells [24, 25]. Employing very short focused ultrasound pulses allows for the simultaneous determination of cell thickness, sound velocity, viscoelasticity, and density [26-28]. One of the main advantages in applying SAM to viable cells is the fact that no prior preparation of the samples is necessary [24, 29, 30].
This review paper describes Time-Resolved SAM (TRSAM) for both image formation using high-frequency focused ultrasound and the acoustic characterization of biomechanical properties. The theory of SAM will be discussed in further detail. Finally, applications of ultrasound biomicroscopy and elastography will be presented with a focus on cancer biology.
2. SCANNING ACOUSTIC MICROSCOPY TECHNIQUES
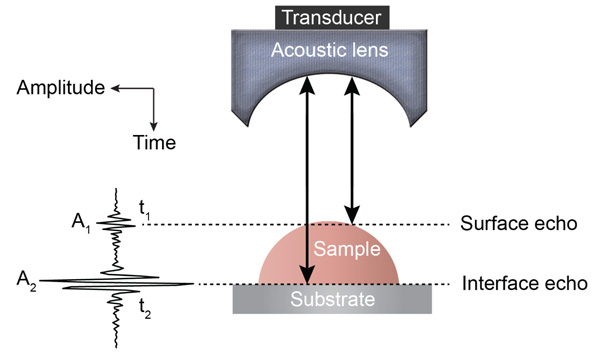
Various SAM techniques have been developed for the mechanoelastic quantification of biological materials on a microscopic cell and tissue level [24, 31]. Detailed descriptions of the fundamental principles of acoustic microscopy have been described elsewhere [26, 31]. In brief, an acoustic pulse is directed and focused onto the specimen through a sapphire lens (Fig. 1). The lens contains a piezoelectric transducer at one end while its opposite side is mounted on a spherical or cylindrical cavity coated with a quarter wavelength of a matching layer [32]. The same lens transmits acoustic pulses and receives the reflected echoes; this is achieved by using a fast electronic switch alternating between the two modes. A liquid, usually a buffered medium (e.g., cell culture medium, phosphate buffer) couples the acoustic lens with the sample.
In one study, acoustic images obtained from chicken heart fibroblasts, recorded at a frequency of 1.5 GHz, revealed protruding bands along the cell margin [33, 34]. Furthermore, it was shown that acoustic images of fibroblasts contained interference fringes similar to Newton rings, which are generated when light is reflected between two surfaces – a spherical surface and an adjacent flat surface. Assuming that the density remains constant, the position and intensities of the rings can be translated into the respective attenuation coefficient, ultrasound velocity, and cell thickness [35]. One main limitation of the so-called Newton ring technique for the acoustic characterization of cells is that interference fringes can only be used for the peripheral area of a cell because the central region lacks fringes. In addition, the order of interference must be known [35]. Errors in the thickness estimation will ultimately translate into errors in the calculation of the respective acoustic attenuation and impedance [36].
In order to determine variations in thickness, density, acoustic wave velocity, stiffness, and the attenuation coefficient of viable or apoptotic cells by SAM, Kundu et al. proposed to use the V(z) technique, that measured voltage (V) versus the defocus distance (z) curve [36]. However, because V(z) curves are only generated when cells remain attached to solid substrates, Rayleigh waves are formed at the angles of incidence. This approach also requires that the surface waves must not be severely attenuated [37]. Due to these limitations, Kundu et al. suggested an alternative technique using V(f) curves [37]. The V(f) approach measures the voltage (V) versus the frequency of sound (f) at a fixed defocus z. One distinctive feature of V(f) curves is that the surface-skimming Rayleigh waves are not generated within the specimen when the acoustic lens is positioned at the focal distance. On the other hand, longitudinal wave speed and attenuation variations within a cell can be predicted using this method [37]. One weakness of the V(f) curve approach is that several parameters (e.g., cell thickness, sound velocity, attenuation) have to be determined from the non-linear curve fitting.
3. TIME-RESOLVED SCANNING ACOUSTIC MICROSCOPY
In contrast to the V(z) and V(f) SAM techniques, the time-resolved approach does not require any of the biomechanical properties of the specimen under investigation to be already known [26, 27, 31, 38, 39]. TRSAM since this acronym has already been introduced in the previous section allows for the determination of the mechanoelastic properties of tissues and individual cells by using highly focused acoustic pulses that are sufficiently short so that reflections from the sample’s surface can be separated from the ones arriving from the interface between the sample and its substrate [27].
The time-of-flight technique was applied in acoustic microscopy nearly thirty years ago [40] to measure the velocity of surface acoustic waves (SAWs) as an alternative to the V(z) curve method. Although its accuracy was estimated to be lower compared to the V(z) curve technique, it permitted measuring the speed of SAWs confined within a small area. Later, a group from Oxford University made an essential contribution to the application of a time-resolving method for layered materials [41-45]. The first measurements of elastic properties of biological tissues at ultra-high frequencies (1.2 GHz) were published by Kanngiesser and Anliker [46]. However, the first results on the elastic properties of single cells by TRSAM were reported by Briggs et al. [27].
3.1. Quantification in Time-resolved Scanning Acoustic Microscopy
In TRSAM, the acoustic parameters of biological cell and tissue samples are derived from the arrival time and the amplitude of the reflected echoes. Fig. (1) shows a typical signal received during the investigation of a sample; two characteristic maxima can be distinguished, A1 and A2, originating from the surface of the investigated specimen and the interface between the specimen and its substrate, respectively. The amplitude of the echoes (A1 and A2) and their respective arrival times (t1 and t2) form the basis for the estimation of local mechanical and elastic properties [26, 47]. The magnitude of the reference signal (A0 ) is reflected from the same substrate material but without any interfering sample along the beam path between the lens and the substrate. The positions and values of the maxima of the echo signals reflected from the surface and the sample/substrate interface can be obtained by using the Hilbert transform H(s) [48], which is described in detail elsewhere [47].
From the amplitude values and the time of arrival, the following parameters can be obtained [29]:
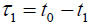 |
(1) |
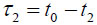 |
(2) |
If the sound velocity in the coupling medium, cw, is known, the measurement of the time delay, τ1, allows for the determination of the cell thickness, d, at any scanning position of the lens (x, y) using a simple geometrical optics formulation as follows [29, 32]:
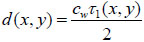 |
(3) |
The time delay, τ1, is also dependent on the scanning position (x, y): τ1(x, y). When the thickness of the cell is known, the longitudinal sound velocity of the specimen is derived by measuring either the time delay τ12:
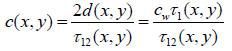 |
(4) |
or the time delay τ2 from the following expressions:
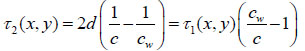 |
(5) |
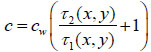 |
(6) |
The coupling medium’s density can be determined empirically with a microbalance at a given volume and temperature. Using the density of the coupling medium, denoted as ρw, and the ultrasonic velocity, denoted as cw, the acoustic impedance, Zw, of the coupling medium can be determined from Eq. (7) as follows [29]:
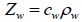 |
(7) |
The ultrasound velocity of the coupling medium (e.g., cell culture medium, phosphate buffer solution) can be calculated based on the empirical formula given by Greenspan and Tschiegg [49] on the assumption that the viscoelastic properties of these media are close to the ones of distilled water at given temperatures.
If A0 is the amplitude of the signal reflected from the fluid/substrate interface, and A1 is the amplitude of the signal reflected from the fluid/cell interface, then the impedance of the cell is given by Eq. (8) [27]:
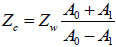 |
(8) |
Therefore, the local density of cells or tissue sections can be obtained using the expression for the ultrasonic velocity and the acoustic impedance given by Eqs. (7) and (8).
Finally, using A2 (amplitude of the interface echo) and A0 (amplitude of the reference echo), the attenuation coefficient of the sample in units of Nepers per unit length can be calculated as follows [27]:
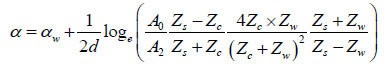 |
(9) |
where Zs is the acoustic impedance of the substrate.
The above analysis, yielding the local biomechanical properties, requires that the echo signals be adequately separated from one another in the time domain. However, if the signals cannot be resolved in the time domain then they can be alternatively expressed in the frequency domain by applying the Fourier transform [26]. From the frequency dependence of A2(f), the frequency dependence of the attenuation can be obtained directly from Eq. (9).
3.2. Theory of Time-resolved Acoustic Microscopy
A detailed discussion of the theory of signal formation in TRSAM is provided elsewhere [42, 50, 51]. The most convenient way to simulate the signal formation in TRSAM is to model a cell or tissue section with a thin liquid layer on a glass substrate. The output voltage of the acoustic lens can be expressed as a function of the lens at a given defocus z and the circular frequency ω [52] using the following analytical expression:
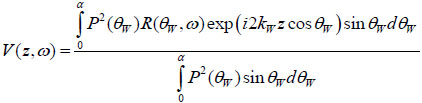 |
(10) |
where, V0 is the signal emitted by the acoustic lens and reflected from a perfectly reflecting surface with P(θW)=1, located on the focal plane (z = 0); α is the semi-aperture angle of the lens,
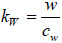 ; cw is the wavenumber in the coupling liquid; z is the defocusing distance; P(θW) is the pupil function of the lens [53]; and R(θW, ω) is the reflection coefficient. V(z, ω) is frequency-independent for a solid half-space, but its behavior depends on the frequency for layered media. The normalizing coefficient
; cw is the wavenumber in the coupling liquid; z is the defocusing distance; P(θW) is the pupil function of the lens [53]; and R(θW, ω) is the reflection coefficient. V(z, ω) is frequency-independent for a solid half-space, but its behavior depends on the frequency for layered media. The normalizing coefficient
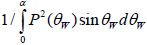 is important when simulating the signal from a sub-surface defect. The sign in the exponent indicates the direction on the z-axis. By convention, the z-axis is directed toward the lens so that any defocusing toward the object, corresponds to a negative value of z.
is important when simulating the signal from a sub-surface defect. The sign in the exponent indicates the direction on the z-axis. By convention, the z-axis is directed toward the lens so that any defocusing toward the object, corresponds to a negative value of z.
The solution for the time-domain output signal in TRSAM is obtained by employing a Fourier spectrum approach. This yields the analytical expression for s(t, z). The acoustic pulse emitted by the lens toward the sample is represented by s0 (t), and the output signal of the acoustic microscope is given by s(t, z). The Fourier spectra of s0 (t) and s(t, z) are denoted as S0 (ω) and S(ω, z), respectively. We assume that the lens is aberration-free and the pupil function is frequency-independent. Therefore the relationship between s0 (t) and s(t, z) and their corresponding Fourier spectra S0 (ω) and S(ω, z) are given by Eqs. (11) and (12):
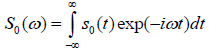 |
(11) |
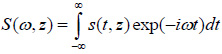 |
(12) |
Due to the linearity of the measurement system, the spectrum of the output signal of the acoustic microscope, S(ω, z), is a product of the spectrum of the input pulse S0 (ω) and the frequency response of the system V(z, ω):
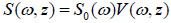 |
(13) |
The echo signal of the acoustic microscope is the inverse Fourier transform:
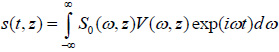 |
(14) |
The shape of s0 (t) of the microscope can be calculated using the following assumptions: (i) the signal reflected from a perfect reflector when the acoustic lens remains in focus is frequency-independent; (ii) the surface of a perfect reflector does not influence the spectrum of the incident beam and, (iii) the echo signal is proportional to s0 (t) for the case when the acoustic lens is in focus [32]. The model uses S0 (ω, z) as measured experimentally for echo signals reflected from a perfect reflector when the lens is in focus. Previous studies have shown that the signal from the glass is a good approximation for s0 (t) when the surface of the glass coincides with the focus of the lens [50].
The calculation of V(ω, z) from Eq. (10) requires knowledge of the pupil function, P(θ), and the reflection coefficient R(ω,θ). Although the pupil function can be determined experimentally (e.g., by scanning a metal ball) [53], typically a rectangular pupil function is used:
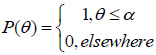 |
(15) |
Bogy and Gracewski obtained an analytical expression of the reflection coefficient for a one-layer system, which can be used for the simulation of V(ω, z) [54-56]. In SAM, the curve V(ω, z) is often called V(f) [37, 57, 58].
It is difficult to obtain an analytical expression for the integral in Eq. (14). However, computational methods allow for the numerical modeling of the propagating short acoustic pulses in TRSAM [59, 60]. Schubert et al. reported the numerical simulation of the acoustic pulse propagation and reflection of the focusing incident waves for different types of scatterers using the elasto-dynamic finite integration technique (EFIT) [61]. In this simulation, the acoustic lens was modeled as a spherical focusing transducer with a half-aperture angle of 60°. The focal length was set at 924 μm emitting a transient (two-cycle raised cosine) pulse at a center frequency of 25 MHz [62]. A water layer was used as the coupling medium (cw = 1500 m/s, ρ = 1000 kg/m3) between the transducer and the boundary fluid. Fig. (2) depicts the results of the simulations for the propagation of short pulses generated by a spherical transducer (Fig. 2A). The reflection of a pulse from a water/steel interface is shown in Fig. (2B and C). Finally, Fig. (2D) shows the propagation of the reflected pulse back to the transducer. The boundary of the half-space is located at the geometrical focal point of the transducer (Fig. 2). If the substrate is an elastic solid (e.g., metal or ceramic), different types of waves can be generated at the water and solid interface. Fig. (2) also demonstrates the generation of shear and longitudinal waves inside a Zn substrate, as well as the generation of Leaky Rayleigh Waves (LRW) and radiation of LRW [62].

These simulations reveal that the incident wavefront has a nearly spherical shape while the reflected wavefront has a more complicated shape suggesting that it is more suitable to use a geometrical optics approach. Such an approach is based on the fact that the main contribution to the signal is made by reflected rays that strike the surface of the transducer normally or rays that intersect the focal point [63-65]. If the inclination of the substrate plane is relatively small, then only rays normal to the substrate should be taken into account for the signal simulations.
4. IMAGE AND CONTRAST FORMATION IN HIGH-FREQUENCY ULTRASOUND BIOMICROSCOPY
High-frequency TRSAM can image biological specimens at a sub-micrometer resolution. Acoustic images are generated from a fixed number of pixels assigned specific greyscale values and coordinates on the image plane (xi, yi), and arranged as a grid. The coordinates (xi, yi) determine the position of each pixel on the grid.
Acoustic images in TRSAM are generated by recording the time-echo signals received from the investigated sample and its substrate. If z is the defocus position of the acoustic lens for when radio-frequency (RF) signals are received and recorded then for each of the pixel coordinates (xi, yi), the measured RF signal can be described as s(xi, yi, z, t). The brightness, I(x, y, z), of each point (xi, yi) on the coordinate system – as recorded at a defocus z – can be described as the integral over time of the squared RF-signal sn(xi, yi, z, t) [66]:
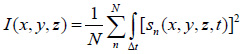 |
(16) |
where, N is the total number of recordings taken at (xi, yi) and Δt is the time gate that covers the delay between the arrival times of the surface and interface echoes. Due to the integration of the signal, sn(xi, yi, z, t), the generated high-frequency acoustic images do not contain any interference fringes characteristic to monochromatic acoustic images [24]. As a consequence, the RF signals contain not only the information necessary for image generation but also intrinsically the information necessary to deduce the elastic and mechanical properties of the sample [31]. Fig. (3) shows C-scan images recorded from HeLa cells. A tenfold averaging of the signals was used to increase the signal-to-noise ratio on these images [47].
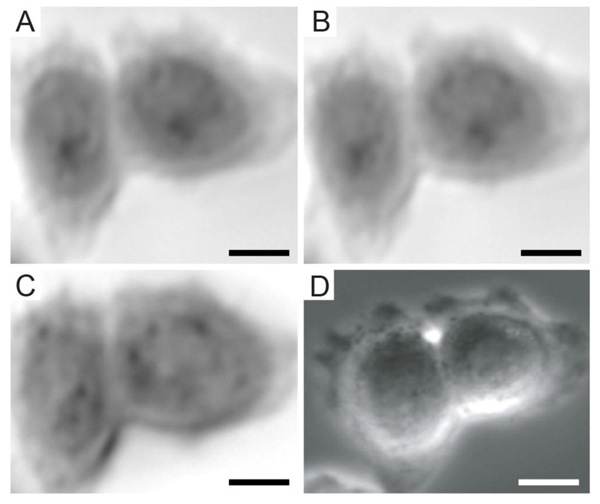
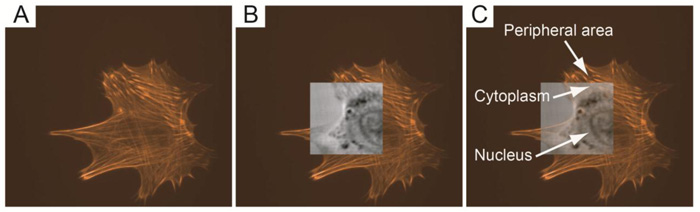
Furthermore, TRSAM allows for the spatiotemporal investigation of dynamic cellular processes, such as the study of focal adhesions. Focal adhesions allow cells to sense and respond to cues in their immediate microenvironment. These protein complexes depend strongly on the interactions between the actin cytoskeleton and integrins [66-70]. In a reported study, the adhesion of embryonic chicken heart muscle cells was investigated by TRSAM [71]. Embryonic chicken heart muscle cells were imaged using brightfield and TRSAM at a center frequency of 860 MHz with a -6 dB bandwidth of 30% [71]. Fig. (4A) demonstrates the advantage of using combined optical and acoustic microscopy concurrently. The contrast in the acoustic images represents the variation of the acoustic impedance and sound attenuation inside the cell [24, 31]. The acoustic images of the embryonic chicken heart muscle cells revealed three distinct areas; the structure that can be clearly identified is the cell nucleus (Fig. 4B and C). Outside the nucleus, in the cytoplasm, numerous small circular shaped organelles can be observed (Fig. 4B and C) that may be liposomes and lipid granules [34]. The appearance of the cell periphery is different compared to the one of the nucleus and the cytoplasm surrounding the nucleus (Fig. 4C).
Besides image formation, TRSAM is capable of quantitative analysis of sound velocity and sound attenuation in cells [72, 73]. During RF data acquisition, the defocus z remains fixed while the RF signals at each pixel position are recorded. This, in turn, allows for the reconstruction of B- and C-scans [47]. The B-scan represents the collection of RF signals when the lens mechanically scans the sample at a fixed defocus z along a single line [31, 74].
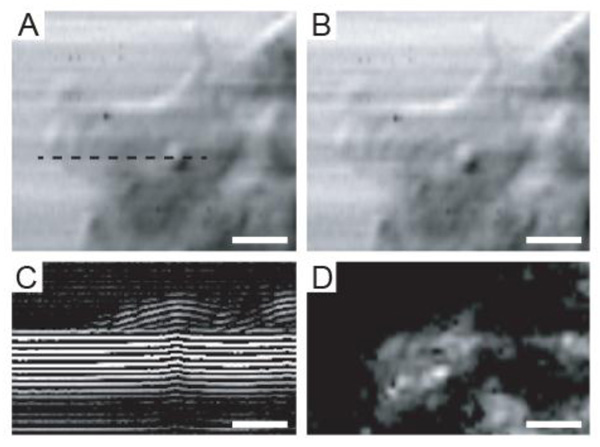
Fig. (5A) shows an intensity image of a viable HeLa cell. The intensity values at each point of the image were obtained using Eq. (16). However, the acoustic image in Fig. (5B) was obtained using a different approach. This image is a single-frequency image and was obtained by choosing the amplitude of the Fourier transform at the central frequency |S(f) = 860 MHz, xi, yi, z)|, where |S| is the amplitude of the Fourier transform of the RF signals: S = F(s(t, xi, yi, z)) measured at each pixel position. The similarity between the intensity- and the single-frequency images is intriguing.
Fig. (5C) is a B-scan derived from the RF signals of the same HeLa cell. The horizontal axis reflects the direction of the B-scan (x is changed while y is kept fixed y = yB). The vertical axis corresponds to the arrival time of individual echoes reflected from the sample back to the transducer. A cross-section of the cell along individual scan lines can be generated by taking the average of the positive part of the RF signals. The intensity of the surface echo is shown in Fig. (5D).
5. APPLICATIONS OF TIME-RESOLVED SCANNING ACOUSTIC MICROSCOPY IN CELL AND TISSUE BIOLOGY
As previously discussed, high-frequency TRSAM is particularly useful when it is required to determine mechanical and acoustic parameters of normal or abnormal cells. TRSAM allows for the observation of spatiotemporal changes of cellular processes under physiological conditions.
Considering that mammalian cells are highly complex structures continually adapting to their microenvironment, the task of determining their biomechanical properties is consequently non-trivial. The many different techniques that have been developed for studying mechanoelastic properties of single cells or tissues contribute each to the collective understanding of cell biomechanics. However, most of these techniques are invasive to various levels and can potentially introduce artifacts due to handling and processing of the specimen. For example, contact by itself may alter cellular responses as it has been established that cells react to mechanical stimuli from their surrounding environment [75]. SAM is among very few techniques that allow for the determination of microstructural properties non-invasively [76, 77].
High-frequency ultrasound studies in the range between 20 MHz and 60 MHz led to the detection of backscatter from single cells. Strohm et al. described an increase of the backscatter intensity for cancerous cells treated with chemotherapeutic agents causing malignant cells to undergo apoptosis [78]. The need to achieve higher resolution and the inability of ultrasound in the range between 20 and 60 MHz to detect the exact sources of backscatter variations, led to the use of ultra-high frequency SAM (e.g., 500 MHz) for the determination of elastic properties of fibroblastic cells whose thickness did not exceed 5 µm [29]. However, even at these ultra-high frequencies, the wavelength of the sound waves was not sufficiently small to resolve internal cell structures. Consequently, higher frequencies in the range between 800 MHz and 1 GHz have been applied in order to discern the acoustic properties of biological specimens at the cell level with a near-optical resolution at a sub-micrometer scale.
Local sound velocity studies have been previously carried out using the time-resolved approach in conjunction with the tone-burst deconvolution technique. In these studies, the sound velocity for human aortic smooth muscle cells under growing, differential, and hypotonic loading conditions was found to be 1571 m/s ± 14 m/s, 1624 m/s ± 16 m/s and 1585 m/s ± 8 m/s, respectively. Similarly, SAM studies of normal coronary artery sections yielded comparable sound velocities of 1560 m/s ± 18 m/s in the medium layer between the intima and adventitia [79].
Cancerous cells differ from normal healthy cells in that they proliferate uncontrollably. Defects in their cell-cycle checkpoints result in the absence of the critical cell control mechanisms that initiate apoptosis, the cell’s programmed death. There is a direct link between the malignant transformation of a healthy cell and its inability to induce apoptosis [80]. This anomaly is accompanied by morphological and mechanoelastic changes [81]. This has triggered a vivid interest in discerning biomechanical properties using TRSAM [47, 82].
HeLa cells [83] were studied using TRSAM for the determination of mechanoelastic properties (e.g., cell thickness, density, attenuation, sound of speed, acoustic impedance) under in vitro conditions [84].
TRSAM on HeLa cells yielded an ultrasound velocity of 1534 m/s ± 33 m/s [47, 85]. Brand et al. estimated the mechanical parameters for viable HeLa cells using a combination of tone-burst excitation with a numerical deconvolution technique [86] instead of the short broadband pulses applied in the TRSAM approach [87].
Brand et al. demonstrated the possibility of combining SAM with deconvolution for the assessment of mechanical and elastic cell parameters. Furthermore, Strohm and Kolios combined TRSAM with the V(z) curve at a frequency of 1 GHz to determine the mechanoelastic properties of viable MCF-7 breast cancer cells [82, 87]. Their findings are summarized in Tables 2 and 3.
Cell monolayers of HeLa cells were studied extensively using TRSAM at a center frequency of 860 MHz with regard to changes in acoustic properties during cell division and adhesion. The study was conducted under physiological conditions using an environment chamber (37°C and 5% CO2). Fig. (6A) shows an acoustic image of HeLa cells taken at a defocus of z = -10 μm. Measurements for determining the sound velocity and attenuation were performed using HeLa cells that were undergoing cell division. Cell (i) (Fig. 6A) has nearly a spherical shape and is probably at the early mitosis stage, while cells (ii) and (iii) have already completed mitosis. Cells that completed division appear with a darker contrast in Fig. (6A), indicating that sound attenuation inside these cells is higher than in cells (i) and (iv). The B-scans of cells (ii) and (iv) are shown in Fig. (6B and C), respectively. B-scan images of HeLa cells at different stages of the cell cycle show distinct patterns inside the cell. The B-scan of cell (iv) has a characteristic hemispherical shape (Fig. 6C). In contrast to cell (iv), the B-scan of cell (ii) reveals a strong signal reflected from the rim surface of the cell (Fig. 6C). Interestingly, the area of strong reflection coincides with the area of increased contrast inside cell (ii). Measurements of the attenuation shown in Table 1 indicate that sound attenuation inside cells increases by a magnitude of approximately 50% after division. Sound velocities of the dividing cells (i, ii and iii) were higher compared to cell (iv) in interphase.

| ROI | A | B | C |
|---|---|---|---|
| Thickness [ µm ] | 12.6 | 15.6 | 11.9 |
| Sound velocity [ m/s ] | 1550 | 1551 | 1548 |
| Density [ g/cm3 ] | 1.239 | 1.120 | 1.306 |
| Attenuation [ dB/cm/MHz ] | 0.020 | 0.031 | 0.021 |
The values for cell thickness, ultrasound velocity, density and attenuation of the parent HeLa cell including the respective daughter cells are summarized in Table 1 for the indicated regions of interest (indicated in Fig. 6A). The RF signals were acquired at a negative defocus of 10 µm below the substrate plane [85]. As mentioned earlier, the attenuation values show a significant increase by approximately 50% within the cytoplasm of the daughter cells. The model proposed by Lizzi et al. offers a valid explanation [88]. This model assumes that a random distribution of weak scatterers correlates with a decrease in the effective scatterer size [88]. This can be attributed to the fact that shortly after the completion of mitosis the internal cell structure re-organizes with many structural elements still scattered throughout the cytoplasm. Another explanation could lie with the acoustic attenuation, which is intrinsically elevated at frequencies above 100 MHz. The nuclear condensation while the cell is in interphase and prepares for mitosis, at which point it eventually divides physically into two daughter cells, could be yet another factor contributing to the sharp increase in attenuation [89]. It was found that sound velocity in differential cells (1624 m/s) was significantly higher than those in growing cells (1571 m/s) and cells on hypotonic loading (1585 m/s). The increase of attenuation coincided with an increase in the acoustic impedance of the cell. Attenuation increases can be attributed to the polymerization of the F-actin [90, 91]. These results are in good agreement with observations made by Kinoshita et al. [89].
Cell thickness, sound velocity, acoustic impedance, density, attenuation, and the bulk modulus of viable MCF-7 breast cancer cells were the focus of a study by Strohm et al. [82]. Acoustic images for the MCF-7 breast cancer cells in interphase and metaphase are shown in Fig. (7). A summary of the mechanical properties for MCF-7 cells are shown in Tables 2 and 3 [82, 87]. The results show an increase in thickness while the cells transition from the interphase to the metaphase with their respective values changing from 11 µm ± 2 µm to 18.9 µm ± 1.3 µm. The same study by Strohm and Kolios showed that the transition of cells from early to late apoptosis was accompanied by a decrease in thickness from 15.3 µm ± 2.4 µm to 12.5 µm ± 2.1 µm [82, 87]. These findings are in agreement with previously reported results for cancer cells undergoing division [85].

| - | Interphase | Metaphase | Water |
|---|---|---|---|
| Thickness [ µm ] | 11.0 ± 2.0 | 18.9 ± 1.3 | NA |
| Sound velocity [ m/s ] | 1570 ± 15 | 1567 ± 11 | 1521 |
| Acoustic impedance [ MRayls ] | 1.561 ± 0.014 | 1.554 ± 0.015 | 1.521 |
| Density [ g/cm3 ] | 994 ± 13 | 992 ± 9 | 1000 |
| Elastic modulus [ GPa ] | 2.45 ± 0.03 | 2.43 ± 0.03 | 2.31 |
| Attenuation [ dB/cm/MHz ] | 1.44 ± 0.15 | 1.10 ± 0.25 | 0.0014 |
| - | Early Apoptosis | Late Apoptosis | Water |
|---|---|---|---|
| Thickness [ µm ] | 15.3 ± 2.4 | 12.5 ± 2.1 | NA |
| Sound velocity [ m/s ] | 1588 ± 20 | 1555 ± 13 | 1521 |
| Acoustic impedance [ MRayls ] | 1.554 ± 0.014 | 1.537 ± 0.009 | 1.521 |
| Density [ g/cm3 ] | 979 ± 13 | 988 ± 7 | 1000 |
| Elastic modulus [ GPa ] | 2.47 ± 0.04 | 2.39 ± 0.03 | 2.31 |
| Attenuation [ dB/cm/MHz ] | 2.00 ± 0.45 | 1.40 ± 0.64 | 0.0014 |

The sound velocity studies for MCF-7 breast cancer cells yielded statistically similar values between interphase and metaphase in the order of 1570 m/s ± 15 m/s and 1567 m/s ± 11 m/s, respectively [85]. Density values were statistically similar between interphase and metaphase on the order of 994 kg/m3 ± 13 kg/m3 to 992 kg/m3 ± 9 kg/m3. However, with regard to the bulk modulus, a statistically significant decrease of 0.02 GPa was found between the interphase and metaphase and an increase of 0.02 GPa between interphase and early apoptosis [85].
During the transition from interphase into early apoptosis, the MCF-7 cells’ thickness increased from 11.0 µm ± 2.0 µm to 15.3 µm ± 2.4 µm [85]. However, an increase in ultrasound velocity was observed between interphase and early apoptosis from 1570 m/s ± 15 m/s to 1588 m/s ± 20 m/s, respectively, followed by a decrease from 1588 m/s ± 20 m/s to 1555 m/s ± 13 m/s when the cells transitioned from early into late apoptosis. A decrease in density was observed between interphase and early apoptosis with the respective values dropping from 994 kg/m3 ± 13 kg/m3 to 979 kg/m3 ± 13 kg/m3. Subsequently, when the cells entered late apoptosis, an increase in density was observed from 979 kg/m3 ± 13 kg/m3 to 988 kg/m3 ± 7 kg/m3. A significantly larger change in the bulk modulus was observed during the cells’ transition from early to late apoptosis on the order of 0.08 GPa [85].
Attenuation values increased from 1.44 ± 0.15 dB/cm/MHz to 2.00 ± 0.45 dB/cm/MHz between interphase and early apoptosis and subsequently decreased from 2.00 ± 0.45 dB/cm/MHz to 1.40 ± 0.64 dB/cm/MHz at later stages of apoptosis [85].
6. DISCUSSION
TRSAM allows for the investigation of elastic and mechanical properties of cells and tissues. Adding the optical and fluorescence component facilitates the correlation of acoustic information with biologically relevant fluorescent markers associated with molecular targets. The arrival times and amplitudes of the echoes originating from the sample and the interface allow for the determination of the local acoustic impedance of cells or tissues. Cells have been modeled as a thin liquid layer on a substrate with spatial variations of elastic properties.
TRSAM has been used for quantitative measurements of mechanoelastic properties at a cell and tissue level. Furthermore, quantitative measurements of the elastic properties of cells in combination with spatiotemporal observation of dynamical cell processes offer enormous potential for characterizing and understanding underlying molecular cues in conjunction with biomechanical properties.
Comparison between the acoustic and fluorescence images of chicken heart muscle cells demonstrated overlap of the actin fibers with the dark bundles that could be seen in the acoustic images indicating that actin fibers can be recognized using TRSAM at ultra high-frequencies. Imaging of focal adhesions in living cells without immunohistological staining is of paramount importance for a wide range of cell biology studies as it provides a tool for investigating spatiotemporal changes in cell locomotion, migration and adhesion.
There is undoubtedly a necessity to determine biophysical features of cells and tissues in a non-nvasive and non-destructive manner. Higher frequencies allow for improved resolution at the expense of penetration depth compared to lower frequencies that facilitate increased penetration depths at the expense of resolution. TRSAM offers a wide range of operating frequencies depending on the requirements determined by the physical dimensions of the samples that need to be characterized.
Biomechanical forces modulate the behavior of cells during intravasation into and extravasation from the vascular system. The emerging recognition of the role of physicomechanical processes in cancer metastasis necessitates the development of novel strategies for bridging the gap toward understanding the interaction between mechanical and biochemical quantities. TRSAM facilitated elastography can contribute toward a more holistic approach that combines biochemical insights with biophysical characteristics. High-frequency ultrasound biomicroscopy and elastography has followed an exciting path thus far bringing together many different fields in basic sciences. The field is marked by a fast-paced development of novel techniques with the potential to translate findings into more efficacious treatment approaches.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The authors would like to acknowledge Michael Kolios and Eric Strohm from the Ryerson University, Toronto, Canada for providing data used in this review article. We would also like to thank Frank Schubert from Fraunhofer IKTS, Dresden, Germany for providing simulation data and intellectual input.


