Unidirectional Influx and Net Accumulation of PIB
Abstract
The compound {N-methyl-[11C]}2-(4’-methylaminophenyl)-6-hydroxybenzothiazole, “PIB”, measured by positron emission tomography, has been demonstrated to image brain β-amyloid deposition in Alzheimer’s disease (AD). In the present study the benefit of measuring the PIB accumulation rate together with the unidirectional influx of PIB into the brain was investigated in healthy control subjects and patients with AD. In a monkey changes in the influx rate constant K1 of PIB closely followed changes in CBF, caused by alteration of PaCO2. In addition, K1 was high both in the monkey and in humans, suggesting that this parameter reflects CBF. Most AD patients studied showed clearly higher accumulation rate for PIB than the controls in cortical brain areas, while a few patients showed as low accumulation as the controls. K1 did not correlate with the accumulation rate, indicating that K1 for PIB provides extra information besides the accumulation rate.
INTRODUCTION
Alzheimer´s disease (AD) is the most common form of neurodegernative disorders and the histopathological definitive diagnosis of AD has been based on the presence of Aβ plaques and neurofibrillary tangles in cortical brain areas at autopsy [1,2]. Amyloid imaging with positron emission tomography (PET) has recently provided new valuable diagnostic tools. The compound {N-methyl-[11C]}2-(4’-methylaminophenyl)-6-hydroxybenzothiazole, “PIB”, has been demonstrated to image brain β-amyloid (Aβ) deposition in AD [3]. In this first report on PIB uptake the average standardized uptake (SUV) in the time interval 40–60 min after tracer administration was used as an index of PIB retention. Later, kinetic analysis was applied on PIB data using reversible models [4]. In another study [5] the need for determination of the input function was eliminated by use of the simplified reference tissue model [6] and the late uptake ratio. The latter measure has also been used in a recent follow-up study [7]. There is presently a rapid development of various amyloid ligands, but so far PIB is the amyloid ligand most widely studied [8].
The primary aim of the present work was to investigate the benefit of combining the information from the rate constant K1 for unidirectional influx across the blood-brain barrier (BBB) with the information from the PIB retention. For this purpose we applied kinetic models requiring input function. In previous studies with kinetic analysis of PIB uptake [4, 5, 9] the distribution volume (DV) or distribution volume ratio (DVR) was chosen as measure of PIB retention. In contrast to this, irreversible kinetic models were applied in the present study and the net accumulation rate constant, Kacc, was chosen as measure of PIB retention in the brain tissue. Arguments for this choice are presented. For comparison with previous studies [5, 7] we also calculated the target-to-reference tissue ratio in a late time interval.
The rate constant K1 for PIB was found to be comparatively large, demonstrating high extraction of PIB into the brain tissue and indicating that this parameter might reflect CBF. Therefore K1 was compared with CBF in a monkey study using PIB and [15O]H2O, first under baseline conditions, and then after an increase of CBF effected by increasing PaCO2 with the aid of respiratory control.
MATERIALS AND METHODOLOGY
Twenty-one patients with a diagnosis Alzheimer’s disease (AD) were included. Of these, 16 patients were included in previous works [3, 7] and 5 were added. The patients had all been referred to the Geriatric Clinic, Karolinska Universty Hospital Huddinge, Stockholm, for memory problems. They underwent assessment for dementia clinical examination including neurological and psychiatric examination, blood analysis, CT or MRI, SPECT, and CSF. The patients fulfilled the criteria for probable Alzheimer’s disease according to NINDS-ADRDA, the National Institute of Neurological and Communicative Disorders and Stroke-Alzheimer's Disease and Related Disorder Association [10]. Their ages ranged from 51 to 81 years. Three young subjects, all 21 years old, and 6 old subjects ranging in age from 59 to 77 years were included in the control group, HC. They had all underwent neurophysiological testings and showed normal cognition for age and education. They were all included as controls in the previous works [3, 7]. The young subjects were included for comparison with the older ones; it is nearly certain that young subjects are free of plaques. The PET-scanning was performed at Uppsala Imanet. A classification of the subjects in the experimental sample was made, based on the ratio between the late uptake of PIB in the frontal cortex and that in the cerebellum. Since only small amounts of Aβ plaques have been found in the cerebellum [11, 12] this region was considered to be a suitable reference region [4, 5, 9].
Experiments in Humans
The Ethics committee of Uppsala University (permissions 01-340 and 02-254), the Karolinska Institute and the Isotope Committee at Uppsala Academic Hospital approved the study. PIB was prepared by the method described previously [13] with modifications described in [3]. Radiochemical purity was greater than 99%. Patients and healthy volunteers were examined after fasting for at least 6 hours before PET. Electrocardiography, pulse and blood pressure were measured throughout the PIB study. The PET camera type used was a Siemens ECAT HR+ (CTI PET-systems Inc., Knoxville TN, USA) with an axial field of view of 155 mm, providing 63 contiguous 2.46 mm slices with 5.6 mm transaxial and 5.4 axial resolutions. Data were acquired in 3D mode. The subjects were given an intravenous injection of approximately 300 MBq of PIB. Uptake in the brain was measured over 60 min divided into 15 frames (2x1 min, 3x2 min, 4x3 min, 4x5 min and 2x10 min). In all subjects the CMRglc was also measured by FDG. The results of these measurements have been reported elsewhere [3].
Attenuation correction was based on a 10-min windowed transmission scan with rotating 68Ge rod sources before administration of the tracers. The emission data were normalized, corrected for random coincidences and dead time, and corrected for scatter using a method described in [14]. Images of radioactivity concentration were reconstructed with the standard software supplied with the scanner (ECAT 7.1), using Fourier re-binning followed by filtered back-projection applying a 4mm Hanning filter.
Image Alignment and Regions-of-Interest
A computerized reorientation procedure was used to align consecutive PET studies for accurate intra- and inter-individual comparisons [15]. Regions of interest (ROI) were drawn in a late FDG summation image (40-60 minutes). The set of ROI was used in previous studies [3, 7, 16]. The thalami were delineated, each with an area of 1.5 cm2, in the slice where they were most clearly visible, and in the same slice a whole brain ROI was formed with ventricles excluded [16]. The temporal region was composed by the summation of the inferior, lateral and medial (anterior and posterior) ROI, and the parietal region was formed by summation of the 4 parietal ROI. In healthy controls PIB is retained only in white matter, making it almost impossible to define the different brain regions in a late summation image (40-60 minutes). In previous studies [3, 7] it was found that an early summation image (6 minutes) with PIB gave an image that could be compared with a late summation image (40-60 minutes) using FDG. The reason is that with PIB the first frames are dominated by blood flow and not retention (see Results and Discussion sections). The early PIB summation image was realigned to the late FDG image and the rest of the PIB activity frames (7-60) minutes were “co-resliced”, using the parameters of the realigned early PIB summation image as template. No correction for partial volume effects was performed.
Determination of the input Function; Metabolite Analysis
Arterial sampling was performed on sub-samples of HC subjects and AD patients. Blood from the radial artery was sampled in 9 AD patients and 4 HC subjects. Of these, 2 belonged to the group of young volunteers (Table 1). During the first 5 min the time course of the tracer in whole blood was measured with a blood sampling system, providing data every sec. In addition, 7 manual blood samples were taken at 2, 5, 8, 12, 25, 45 and 60 minutes after bolus injection. In 4 experiments sampling was at 10 min in place of 8 min, in 5 experiments sampling was at 15 min in place of 12 min and in 2 experiments one sample was taken at 30 min in place of two at 25 and 45 min. These whole blood samples were centrifuged and the proteins precipitated. The protein-free fraction was analysed by high performance liquid chromatography (HPLC) in regard to metabolism of PIB. Separation of metabolites and tracer was performed on a Genesis C18 column. The radioactivity in the metabolite and tracer fractions as well as the radioactivity in whole blood and plasma was measured in a well counter. The blood sampling system, the well counters, and the positron camera were cross-calibrated in advance. The fraction of unchanged tracer in plasma at the measuring times used in the blood sampling was estimated by linear interpolation. The time course of the unchanged tracer concentration in arterial plasma was subsequently used as the input function.
Monkey Experiment
Experiments with PIB and [15O]H2O were performed in a rhesus monkey. The Animal Ethics Committee of Uppsala University approved the experimental protocol (C117/04). The same scanner was used as for the experiments on humans. Before PET, the monkey was anaesthetised with Propofol and maintained on anaesthesia by Sevoflurane inhalation during the experiment. Two PET scans, first with [15O]H2O and 15 min later with PIB, were performed under baseline conditions. Two hours after the end of the PIB scan CBF was increased by increasing PaCO2 with the aid of respiratory control, and thereafter another two PET scans with [15O]H2O and PIB were performed. For the scans with [15O]H2O the injected doses were close to 330 MBq and the scan duration in both cases was 60 sec divided into 12 frames each of 5 sec duration. The radioactivity in whole blood was measured with the same type of blood sampling system as used for the measurements on humans. For the scans with PIB the injected doses were 140 MBq and the scan duration in both cases was 60 min, with the same frame division as used in the human study. Blood samples were taken at the same times and analysis of the data was performed in the same way as in the human study.
Regions of interest, defining thalamus and frontal, occipital and cerebellar cortices, were drawn manually. Summed images of early kinetics (0-8 min) were used to delineate cortical regions while late summations (40-60 min) were used to identify the thalamus. As for the human images, the ROIs were delineated in several consecutive slices and were afterwards summed up to a volume of interest.
KINETIC MODELS APPLIED
Using [3H]PIB the specific binding to human brain homogenate was found to be reversible with an off-rate half life of 252 min [4]. Accordingly, the effect of dissociation from specific binding of PIB must be small during the 60 min data acquisition time used in the present study. Indeed, as will be shown in the Results section, uptake during the data acquisition time was found to be dominated by accumulation/binding with few or no observable effects of dissociation. Based on these observations, mainly irreversible kinetic models were applied in the present study. The Gjedde-Patlak model [17, 18] was applied, because this method gives an indication of how well the tracer can be described by irreversible kinetics. Further, the irreversible two compartment model with 3 rate constants, ”input-3k “ mode,l was applied and compared to the reversible two compartment model with 4 rate constants, ”input-4k” model. These models require experiments with arterial sampling. As comparison a method utilizing the target-to-reference ratio in a late time interval,” late uptake ratio”, was applied, because this measure has been utilized in previous works [5, 7] and is of interest for clinical studies. The kinetic models applied on PIB data are further described in the Appendix. For construction of CBF maps from the scans with [15O]H2O in the monkey, the model described by Raichle et al. [19] was applied.
Statistical Methods
The three compartment models applied on the PIB data were compared statistically with the aid of the F-statistics [20]. Often the so called Akaike- and Scwartz criteria are also used in this context, but all three measures are based on the same quantity – the sum of residuals squared – and is accordingly strongly coupled. The different measures of PIB uptake provided by the applied models were compared through the regional contrast obtained between two selected groups of experiments. The groups chosen were the HC group (n=3) on the one hand and the AD patients with high PIB uptake in cortical areas (“AD-Hi”, n=5) on the other. The selection of these groups is described in the results section Only experiments with arterial sampling were considered. As a measure of contrast the “standardized difference” was used. For each index and region the standardized difference (m1-m2) / √(SD12+SD22)/2 was calculated from the sample means m1, m2, and the sample standard deviations SD1, SD2 for the two groups [21].
RESULTS
General Observations
Fig. (1a and b) show the distributions of the late uptake ratios for the frontal cortex in the HC and AD groups, respectively. Cerebellum was used as reference region and data from the time interval 40 - 60 min were used. The highest ratio (1.75) in the HC group was found in the oldest subject (77 yr), who also had a slightly higher late uptake ratio in the parietal cortex than the other controls. This control subject showed normal performance in cognitive tests except for some difficulties in copying a complex cube [3]. The subject was retested 2 years later with still normal cognitive performance [7]. The value 1.75 is 5.8 standard deviations from the average ratio of the remaining 8 controls (average 0.99, SD 0.13). Based on these observations this control subject is treated separately in the following and denoted “HC-Hi”. For the remaining HC group the late uptake ratio was below 1.3 (cf. Fig. 1a). One subject originally recruited as control was found to have a high uptake ratio in the frontal cortex (2.26) as well as in other cortical areas. In addition this subject showed abnormal performance when assessed in comprehensive cognitive tests and was therefore removed from the control group and classified as “Hi”.
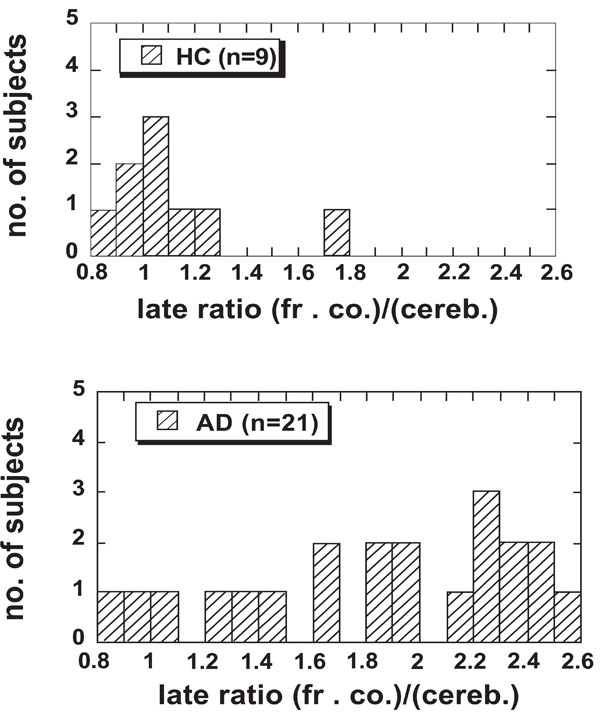
The late uptake ratio in the frontal cortex for the HC group (n = 8) together with the single HC-Hi subject (the entry with the highest value) and all AD patients (n = 21). Data in the time interval 40–60 min were used.
Fig. (1) shows that for most of the AD patients the late uptake ratio in the frontal cortex was higher than for the control subjects. In addition, some of the AD patients showed equally low uptake ratio for PIB in the frontal cortex as the HC subjects. These patients also showed very low uptake ratio in other cortical areas examined [3], and in this respect they could not be distinguished from the control subjects. Owing to the observed large variation in PIB late uptake ratio in the frontal cortex and other areas, a presentation of mean values for the whole AD group is misleading and makes comparison between different measures of PIB retention difficult. Therefore, based on the distribution of the late uptake ratio in the frontal cortex, the sample of AD patients was split into two groups. The upper limit of the late uptake ratio in the HC group, 1.3, was chosen as reference value. The AD patients with a ratio below 1.3, the “AD-Lo” group, contained 4 subjects. The AD patients with a higher ratio were placed in the “AD-Hi” group and consisted of 17 subjects. Data for the groups according to this classification are summarized in Table 1. The subject who was removed from the control group and classified as “Hi” is also included in the table.
Clinical data of the subjects in the study classified into different groups as explained in the text. For age and MMSE, mean value, standard deviation and range are presented. The different groups are defined in the text. MMSE = mini-mental state examination
| Groups | No. of Subjects | Age at Study Mean (SD) Range | Arterial Sampling | MMSE at Study Mean (SD) Range |
|---|---|---|---|---|
| HC-young | 3 | 21 (0) | 2 | 30 |
| HC-old | 5 | 67 (7) 59–77 |
1 | 30 |
| HC-Hi | 1 | 77 | 1 | 30 |
| Hi | 1 | 71 | 1 | 30 |
| AD-Lo | 4 | 72 (11) 58–81 |
3 | 28.3 (0.5) 28–29 |
| AD-Hi | 17 | 65 (9) 51–80 |
5 | 22.7 (4.7) 9–27 |
Results of Human Experiments with Arterial Sampling; Accumulation Rate
Figs. (2) show examples of Gjedde–Patlak distributions for frontal cortex in one HC- and one AD-Hi subject. Before calculating the x and y variables in the plots, the uptake data were corrected for vascular contribution using Eq.1 in the Appendix. For frontal cortex the value 0.04 was used for CBV, whereas the value 0.02 was used for white matter. The distributions illustrate two general features of most of the data distributions in the Patlak plots. First, the late parts of the data distributions were in most cases well described by straight lines. The straight lines displayed were fitted to the data in the time interval 30–60 min. The data points to the right of the vertical dashed line were used in the fit. The r-values of the line fits fell in the range 0.86–1.0 with an average of 0.97 and SD 0.03. Second, the slope values were in general positive, indicating that there was a positive accumulation rate of PIB in all investigated regions.
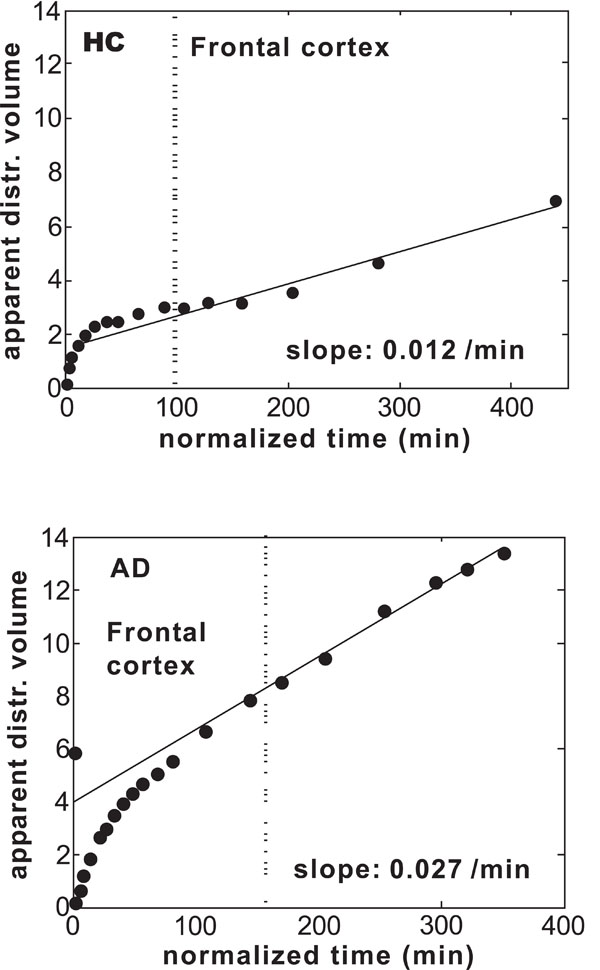
Gjedde–Patlak plots for frontal cortex in (a) one subject in the HC group and (b) one patient in the AD-Hi group. The straight lines were fitted to the data in the time interval 30–60 min.
Some exceptions to these two observations were found. For one patient in the AD-Lo group the cerebellar cortex, thalamus, pons, and even temporal cortex were found to have negative slopes. In addition, the data distribution in the Gjedde–Patlak plot for white matter was slightly concave, and the slope value was far below the values found for this region in all the other experiments with arterial input. In one HC subject only manual blood sampling was performed, which easily results in a bad determination of the input function. For this subject the slope values were considerably lower than for the other subjects in the HC group and the slope values were negative in the putamen and the thalamus, but positive in the cerebellar and temporal cortex. In two patients the distribution in the pons could not be well described by a straight line, and for one of these patients the distributions in the thalamus and putamen could not be well described by straight lines after 30 min.
Fig. (3) shows examples of applying the irreversible two-compartment model with three rate constants and input function (input-3k model) to the frontal cortex in one HC subject and one AD patient. The same uptake data as in Fig. (2) were used. In each figure the lower solid line is the vascular contribution. The dashed line is the contribution from the first compartment (free tracer in tissue); the dotted line is the contribution from the second compartment (bound tracer in tissue); the upper solid line is the total model prediction. The experimental data are presented as a stacked histogram.
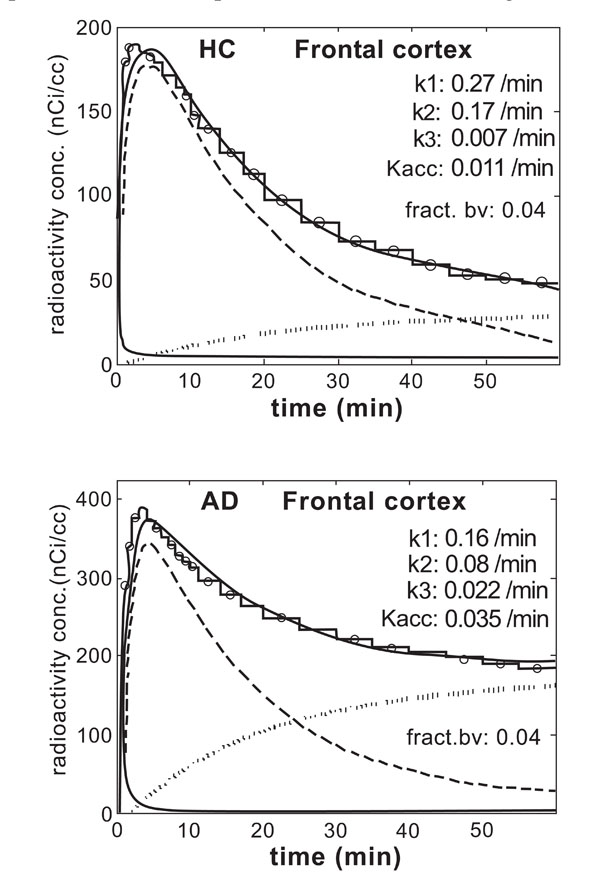
The result of applying the irreversible two-compartment model (three rate constants, input-3k model) to frontal cortex in one HC subject and one patient in the AD-Hi.
Clearly the fits were not perfect. The model failed to reproduce well the initial large slope of the uptake and the subsequent decrease, but described the final part of the data distribution well. These features of the model were common to all regions in all experiments.
The data in Table 2 show that the Kacc values obtained with the input-3k model were similar in the HC and AD-Lo groups, especially in the cortical regions. In comparison, higher Kacc values were obtained in the AD-Hi group in all selected regions. The largest differences were found in the frontal and parietal cortex. In the cerebellum the Kacc values for both the HC- and AD-Hi groups were comparatively low and similar, 0.014±0.005 and 0.017±0.004 min-1 respectively, justifying use of the cerebellum as a reference region. For the outlier HC-Hi the Kacc values in the cortical areas systematically fell between those found in the HC- and AD-Hi groups. A comparison of the regional values obtained for each group shows that in the AD-Hi group the highest parameter values were found in frontal– and parietal cortices,and the values of the visual- and temporal cortex were higher than or close to the values in white matter. In contrast, in the HC- and AD-Lo groups the highest values were found in white matter and pons. The rate constant k3 (not presented), obtained with the input-3k model, showed a regional pattern close to that of Kacc. The slope values from the Gjedde–Patlak analysis (not presented) had almost the same regional pattern as the Kacc values obtained from the input-3k model.
The accumulation rate constant Kacc from the irreversible 2-compartment model “input-3k” and the unidirectional influx rate constant K1 from the reversible 2-comartment model “input-4k” in selected regions. Means and SDs are presented. The different groups are defined in the text. The standardized difference is described in the text
| Region | Used CBV | Kacc (min-1) from irreversible 2-compartment model (input-3k) | K1 (min-1) from reversible 2-compartment model (input-4k) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HC (n=3) | HC-Hi (n=1) | Hi (n=1) | AD-Lo (n=3) | AD-Hi (n=5) | Stand diff AD-Hi-HC | HC (n=3) | HC-Hi (n=1) | Hi (n=1) | AD-Lo (n=3) | AD-Hi (n=5) | Stand. Diff.AD-Hi- HC | ||
| Whole brain | 0.035 | 0.0175 0.0046 |
0.0185 | 0.0274 | 0.0156 0.0016 |
0.0326 0.0039 |
3.55 | 0.28 0.05 |
0.18 | 0.20 | 0.18 0.03 |
0.18 0.04 |
-2.34 |
| PrVisual cortex | 0.05 | 0.0127 0.0041 |
0.0152 | 0.0223 | 0.0124 0.0021 |
0.0359 0.0080 |
3.65 | 0.38 0.04 |
0.23 | 0.28 | 0.24 0.08 |
0.27 0.06 |
-2.15 |
| Frontal cortex | 0.05 | 0.0136 0.0031 |
0.0221 | 0.0367 | 0.0145 0.0022 |
0.0389 0.0062 |
5.19 | 0.31 0.04 |
0.19 | 0.23 | 0.19 0.02 |
0.20 0.06 |
-2.26 |
| Parietal cortex | 0.05 | 0.0148 0.0036 |
0.0212 | 0.0313 | 0.0148 0.0024 |
0.0369 0.0050 |
5.04 | 0.32 0.04 |
0.20 | 0.20 | 0.19 0.04 |
0.16 0.05 |
-3.46 |
| Temporal cortex | 0.05 | 0.0140 0.0040 |
0.0151 | 0.0235 | 0.0132 0.0020 |
0.0306 0.0040 |
4.19 | 0.27 0.05 |
0.17 | 0.17 | 0.15 0.02 |
0.15 0.02 |
-2.93 |
| Putamen | 0.04 | 0.0119 0.0037 |
0.0148 | 0.0293 | 0.0149 0.0023 |
0.0358 0.0023 |
7.80 | 0.40 0.03 |
0.27 | 0.30 | 0.26 0.03 |
0.30 0.05 |
-2.56 |
| Thalamus | 0.04 | 0.0132 0.0056 |
0.0137 | 0.0274 | 0.0112 0.0037 |
0.0243 0.0026 |
2.56 | 0.35 0.04 |
0.25 | 0.30 | 0.25 0.04 |
0.30 0.09 |
-0.68 |
| Pons | 0.02 | 0.0186 0.0062 |
0.0159 | 0.0250 | 0.0197 0.0027 |
0.0246 0.0053 |
1.03 | 0.32 0.06 |
0.19 | 0.23 | 0.19 0.04 |
0.29 0.14 |
-0.26 |
| White matter | 0.02 | 0.0250 0.0030 |
0.0225 | 0.0179 | 0.0219 0.0015 |
0.0312 0.0048 |
1.56 | 0.17 0.05 |
0.13 | 0.07 | 0.09 0.03 |
0.10 0.02 |
-2.03 |
| Cerebellar cortex | 0.05 | 0.0137 0.0051 |
0.0086 | 0.0110 | 0.0107 0.0006 |
0.0169 0.0042 |
0.69 | 0.38 0.04 |
0.25 | 0.32 | 0.22 0.04 |
0.24 0.04 |
-4.79 |
The F-test showed that the input-4k model, achieved by allowing dissociation of bound PIB, gave a significantly improved fit (p <0.001) compared with the input-3k model for nearly all (121) of the 130 investigated uptake curves. In particular, the input-4k model gave a better fit of the initial peak in uptake, but on the other hand the model often could not describe the late part of the uptake so well, where positive residuals were often obtained. The uptake was found to be well described by the irreversible input-5k model in all selected regions for all experiments. In particular the positive residuals, often observed at late times with the input-4k model, were absent with the input-5k model. An F-test also showed that addition of a fifth parameter resulted in significant improvement compared to the input-4k model for most of the uptake curves, although the improvement was much less pronounced than after addition of a fourth parameter to the input-3k model. For 7 time-activity curves out of 130 the fit gave k5 = 0, indicating that addition of a third compartment resulted in no improvement at all.
In agreement with [4] the fraction of labelled metabolites was found to be large at the end of the scan time (over 90% of the measured radioactivity at 60 min), which implies that the estimate of unchanged tracer in this time period became sensitive to decay fluctuations, background detection, and systematic errors. As an extreme example, if the fraction of unchanged tracer at 60 min was decreased from 3% to 2%, the estimated accumulation rate increased by 10%, whereas an increase of unchanged tracer at 60 min from 3% to 4% decreased the accumulation rate by 13%.
Relative Uptakes at Late Times
Table 3 shows the group means of the late uptake ratio for the subjects with arterial sampling. A comparison with the data on Kacc in Table 2 shows that similar regional patterns were obtained with the two parameters. For a given region the subject HC-Hi had as a rule somewhat higher parameter value than found in the HC- or AD-Lo group and the Hi subject had a still higher value, close to the value found in the AD-Hi group. Exceptions from this ordering were found in pons and white matter (and in cerebellum in case of Kacc). In these regions there is no or very small amounts of Aβ and therefore one cannot expect the same pattern as in regions rich of Aβ in AD patients.
Ratio between average uptakes in the target region and cerebellar cortex using data in the time interval 40–60 min (late uptake ratio). The groups are defined in the text. Only patients with arterial sampling are included. Means and SDs of the samples are presented. The standardized difference is described in the text
| region | Cobs(target)/Cobs(cereb) averaged over the interval [40–60min] | |||||
|---|---|---|---|---|---|---|
| HC (n=3) | HC-Hi (n=1) | Hi (n=1) | AD-Lo (n=3) | AD-Hi (n=5) | Stand diff (AD-Hi – HC) | |
| Whole brain | 1.27 0.29 |
1.52 | 1.74 | 1.16 0.09 |
1.68 0.30 |
1.96 |
| PrVisual cortex | 1.06 0.29 |
1.32 | 1.47 | 1.01 0.13 |
1.78 0.52 |
2.42 |
| Frontal cortex | 1.05 0.22 |
1.75 | 2.26 | 1.11 0.17 |
2.02 0.47 |
3.75 |
| Parietal cortex | 1.14 0.19 |
1.72 | 1.94 | 1.15 0.19 |
1.93 0.31 |
4.35 |
| Temporal cortex | 1.13 0.20 |
1.40 | 1.59 | 1.09 0.12 |
1.64 0.26 |
3.06 |
| Putamen | 1.08 0.29 |
1.43 | 1.94 | 1.27 0.20 |
1.90 0.30 |
3.92 |
| Thalamus | 1.30 0.39 |
1.38 | 2.14 | 1.26 0.25 |
1.53 0.32 |
0.91 |
| Pons | 1.63 0.18 |
1.54 | 1.52 | 1.68 0.16 |
1.53 0.11 |
-0.87 |
| White matter | 1.62 0.31 |
1.81 | 1.73 | 1.44 0.15 |
1.63 0.30 |
0.05 |
No clear difference in late uptake ratio could be detected between the young and old healthy controls. When also subjects without arterial sampling were included in the comparison, the mean and SD of the late uptake ratio for the whole brain was 1.23 (SD 0.31) for the HC-young group (n=3) and 1.29 (SD 0.22) for the HC-old group (n=5). In comparison, for the AD-Hi group (n= 17) the ratio was 1.65 (SD 0.22).
Results of Human Experiments with Arterial Sampling; Unidirectional Influx
The regional K1 values found with the input-4k model are summarized in Table 2. These values were consistently higher in all regions than the corresponding values obtained with the input-3k model (not shown). Because the 4k-model fitted the initial part of the uptake data better than the input-3k model, the K1 values obtained with the input-4k model should give a better description of the transport of PIB across the BBB. Very similar regional contrasts in K1 were obtained with the input-3k and input-4k models. Typical CBF values measured with PET in HC subjects are 0.6 ml ml-1 min-1 in cortical areas, 0.2 ml ml-1 min-1 in white matter and 0.5 ml ml-1 min-1 in whole brain [22]. Thus the obtained K1 values indicate that the first pass extraction fraction (K1/CBF) of PIB was above 50%.
The data in Table 2 show that in all selected regions the K1 values were higher in the HC group than in the AD-Lo and AD-Hi groups. The relative differences between groups were somewhat smaller in K1 than in Kacc, but statistically the differences were highly significant. From the null hypothesis of equal values in the two groups(HC and AD) in all regions, and using the binomial distribution, the probability of observing the same sign of the average difference in 9 regions selected in advance is 0.002. No difference in K1 between the AD-Lo and AD-Hi groups was detected. It should be observed that the oldest control subject (HC-Hi), who was found to have enhanced PIB retention in the frontal and parietal cortex (see Fig. 1 and Table 2), had lower K1 values than the average in the HC group in all investigated regions. Also the subject classified as “Hi” had lower K1 values than found in the HC group. Thus, the subjects with enhanced PIB accumulation also had lower K1 than the HC group in the cortical regions. In addition 3 patients without enhanced PIB accumulation had decreased K1 compared to the HC group.
Contrast Between Groups
The standardized difference between the parameter values for the HC and AD-Hi groups, used as a measure of contrast achieved with the different methods of quantification, are presented in Tables 2-4. Clearly, the contrast was considerably larger with Kacc than with k3 (not shown) or with the late uptake ratio in all regions except the visual cortex. In most regions the late uptake ratio showed greater contrast than k3. The contrasts using different measures were clearly correlated; a region with high contrast in Kacc tended to show high contrast in the late uptake ratio as well. This was expected, because the regional pattern in a Kacc map resembled the pattern in the corresponding map of average uptake in the interval 40–60 min (not shown).
Results from the monkey experiment. Base: baseline experiment, CO2: experiment with increased CBF caused by increased PaCO2 with the aid of respiratory control. The models applied are described in the text
| Region | CBF (ml g-1 min-1) | K1 input-3k (ml g-1 min-1) | Kacc input-3k (min-1) | k3 input-3k (min-1) | Late uptake ratio | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Base C | O2 Ba | se | CO2 Ba | se | CO2 Ba | se | CO2 Ba | se | CO2 | |
| Cerebellar cortex |
0.38 |
0.68 |
0.29 |
0.55 |
0.029 | 0.034 | 0.013 | 0.012 | 1.00 | 1.00 |
| Frontal cortex | 0.30 | 0.46 | 0.24 | 0.37 | 0.021 | 0.027 | 0.012 | 0.014 | 0.77 | 0.84 |
| Occipital cortex |
0.36 |
0.66 |
0.29 |
0.58 |
0.026 | 0.034 | 0.012 | 0.013 | 0.94 | 1.03 |
| Thalamus | 0.28 | 0.54 | 0.18 | 0.35 | 0.026 | 0.032 | 0.008 | 0.008 | 1.29 | 1.21 |
Parametric Maps
Fig. (4) shows parametric maps of the accumulation rate constant Kacc and the influx rate constant K1 for one young HC subject and one patient in the AD-Hi group. The linear integral method for parameter estimation [34] was used together with the irreversible input-3k model with input function. The image slice was placed in roughly the same position in the two brains. A trans-axial slice at the level of the head of caudate nuclei is displayed. The maps of Kacc demonstrate the large difference found between the HC group and the majority of the AD patients in the regional distribution of this parameter. For the HC subject the Kacc distribution gave mainly a map of white matter. In the AD patient the highest net accumulation rate was found in the posterior cingulum. The K1 maps illustrate the data in Table 2; on average the AD patients had lower K1 values than the HC subjects in all regions. The K1 image from the AD patient shows that in this case especially low values were obtained in parts of the frontal and parietal cortex.

Parametric maps for PIB. Data from the same two experiments as in Fig. (2) were used. The maps show Kacc (left column) and K1, (right column) for one HC (upper row) and one AD-Hi subject (lower row). For Kacc the colour scale goes from 0.01 to 0.055 min-1, and for K1 the scale goes from 0.0 to 0.5 min-1.
Results from the Monkey Experiment
The results of kinetic analysis in the monkey experiment are summarized in Table 4. As an effect of respiratory control PaCO2 changed from an average of 5.0 (SD 0.2) kPa during the two baseline experiments to an average of 7.2 (SD 0.1) kPa during the two later scans. Using the found values, first pass extraction fraction (K1/CBF) was calculated to be 77% (SD 8%) on average. The tabulated data show that the regional increases in CBF were between 53 and 93%. The corresponding increases in K1 were of the same order, between 50 and 100%. The increases in Kacc were smaller; in the range 17 to 31%, and the increases in k3 values were smaller; in the range 0 to 17%. Qualitatively, these results were to be expected, because ideally k3 is independent of CBF, whereas Kacc depends on CBF via K1 and k2. The data in Table 4 show that the increase in the late target-to-reference ratio was less than 10%.
Fig. (5) shows maps of CBF, K1 and Kacc in one slice of monkey brain under baseline conditions and after increased PaCO2. The monkey was anaesthetised and therefore its position was the same during all four scans. The maps illustrate the very large increases in CBF and K1 values caused by the changed PaCO2. The regional increases in K1 were of the same magnitude as the increases in CBF and the regional patterns in CBF and K1 were similar before and after the increase. These results indicate that K1 for PIB to a large extent reflects CBF. Comparison of the K1 and Kacc images showed that PIB, as in humans, mainly accumulates in white matter inside the cortex, but clearly there were considerable partial volume effects in the monkey images. The increase in Kacc as an effect of the increase in CBF was detectable, but small compared with the increase in K1.
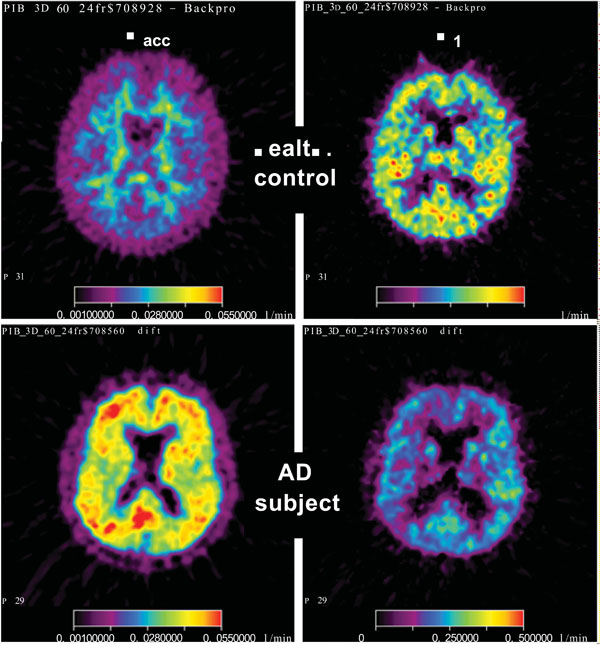
Parametric maps from one brain slice in the monkey experiment. The upper row shows maps from the baseline experiments (from the left: CBF, K1, Kacc), and the lower row shows the corresponding maps after increased PaCO2. For CBF the colour scale goes from 0.02 to 0.7 ml g-1 min-1, for K1 the scale goes from 0.04 to 0.7 min-1, and for Kacc the scale goes from 0.01 to 0.07 min-1.
DISCUSSION
The Choice Between Models Describing Irreversible or Reversible Kinetics
As illustrated in Fig. (2) and indicated by the r-values, the data distributions in the Gjedde–Patlak plots were fairly well described by straight lines in the time interval 30–60 min. Tracers with irreversible kinetics show this pattern [23]. These results do not imply that reversible kinetics can be excluded, because the data distribution in the Gjedde–Patlak plot is insensitive to small deviations from irreversible kinetics. However, the observed distributions do indicate that the tracer was far from being in equilibrium conditions and also that the time course of PIB in the brain was dominated by accumulation in the time interval 0–60 min. As a consequence there was very little information about dissociation of PIB in the time-activity data. PIB was designed to bind reversibly, but the measured dissociation rate has been found to be slow. In measurements on human brain homogenate with [3H]PIB the dissociation rate constant for specifically bound PIB was determined to be 0.0028 min-1, corresponding to an off-rate half-life of 252 min [4]. Further, using real-time in vivo multi-photon microscopy in transgenic mice, it was shown that although unbound PIB rapidly cleared from the normal brain parenchyma, bound dye remained associated with amyloid deposits for several days [24]. The general shape of the Gjedde-Patlak data distributions obtained in this study is consistent with these previous results.
Concerning the cases where the Gjedde-Patlak distributions clearly deviate from the straight-line behaviour of, it must be remembered that, presently, the mechanism for binding of PIB is not well understood. The reason for deviations from the general behaviour might be that the time for equilibrium is different in different regions and subjects.
In comparison with the above, it is known that the phosphorylation of FDG is a reversible process, but the corresponding k4 (cf. eqs 2 and 3) has been found to be small, 0.0055 min-1 (SE 0.0003) in human grey matter [25], but yet the Gjedde–Patlak distributions for FDG are well described by straight lines in the time interval 20–60 min. By confining the FDG measuring time to less than one hour the effect of dephosphorylation can be neglected and irreversible models can be used. As the estimated k4 for PIB is a factor of two smaller than that for FDG, it is appropriate to neglect the effect of k4 during the first hour after administration of PIB and apply irreversible kinetics in this time interval.
In a previous study [4] the reversible Logan method, using either input function [26] or reference tissue [27], was applied. The time course of the tracer was followed for 90 min, i.e. 50 % longer time than in the present study. Despite the slow dissociation rate the data distributions in the Logan plot for PIB fell approximately along straight lines at late times. However, it is questionable if these slope values give accurate estimates of DV (with input function) or DVR (with reference region), because the slope in these graphs is an estimate of the target-to-reference ratio at equilibrium, which occurs a long time (in the order of 3 half times [4] or more than 10 hours) after the end of the measurements. Thus, the time-activity data during the first hour must give very poor estimates of DV or DVR of PIB. Like the late uptake ratio, the slope in the Logan plot reflects variations in the accumulation rate of PIB.
The choice of model must be based on already known features of the tracer. In the case of PIB the equilibrium between bound and unbound tracer will occur a long time after the end of the PET measurements, and therefore it is inappropriate to apply a model such as the simplified reference tissue model [6] which assumes instantaneous equilibrium between free and bound tracer after administration. Results [5] from application of such a model can easily be misleading. The applied models must not be at variance with basic observations.
Choice Between Measures of PIB Accumulation
Irreversible models provide measures of PIB accumulation, whereas reversible models provide measures of PIB retention. In the input-3k model the rate constant for binding (k3) is assumed to be directly proportional to A β deposition and should in theory be a better index of binding than the net accumulation rate constant Kacc, which, besides k3, also depends on transport across the BBB. However, unlike k3 which depends on the structure of the operational equation for the model and is more sensitive to noise, Kacc is directly coupled to the shape of the uptake curve at late times. It was found that the contrast between the AD-Hi and HC groups, measured by the standardized difference of the means, was considerably worse with k3 than with Kacc. Thus the latter parameter was found to be a better measure of PIB accumulation than k3.
For large clinical investigations the use of late uptake ratio is attractive because there is no need of arterial sampling, the computations become simple and the subjects need to be placed in the camera for only a limited time interval. The data presented in Tables 2 and 3 show that, with the standardized difference as index, the late uptake ratio gave less contrast than Kacc in all areas examined. This result is not surprising; during the first hour after tracer administration the time course of PIB is dominated by accumulation and consequently Kacc is an adequate measure of PIB uptake.
The monkey experiments provided information about the sensitivity of the examined measures of PIB accumulation as regards changes in CBF. As expected, Kacc was more sensitive to CBF changes than k3 or the late uptake ratio, because the former parameter is, via K1 and k2, dependent on the transfer of tracer across the BBB, and this transfer is flow-dependent. If both the uptakes in the target- and reference regions are flow dependent as observed in this study, the late uptake ratio will be insensitive to flow changes because the flow dependence will tend to cancel between numerator and denominator. In the monkey an increase of CBF with 53 % caused an increase in Kacc with 29 % in the frontal cortex (Table 4). For the same region in humans K1 was 35% lower, but Kacc was 184% higher in the AD-Hi group than in the HC group (Table 2). Thus, for PIB the effect of Aβ binding dominates over the effect of low CBF. The experiments were performed under anaesthesia, but it is highly improbable that the observed coupling between K1 and CBF should not persist without anaesthesia.
The Relationship Between CBF and Unidirectional Uptake of PIB - Combined Information on PIB Influx and Net Accumulation
The use of K1 for PIB as an index of CBF is based upon three properties of PIB uptake in the brain: (1) first pass extraction is relatively high (>50%), (2) the tracer probably enters and leaves the brain via passive diffusion, and (3), in- and out-flux across the BBB dominate the initial uptake of PIB, implying that binding does not disturb the determination of K1 to any appreciable extent (cf. Fig. 3). The results of the monkey experiments (Table 4 and Fig. 5) indicated that the regional distributions of K1 and CBF were similar. The changes in K1 were found to closely follow the changes in CBF.
The data in Table 2 show that the AD patients had lower K1 values than the HC subjects in the selected areas and, based on the results of the monkey study, must be interpreted as a difference in CBF between the AD- and HC groups. This conclusion is in accordance with results from previous studies of CBF in AD patients [28, 29, and 30]. It could be argued that the difference in K1 found between the AD patients and the HC subjects was due to an age effect, because 2 of the 3 HC subjects examined with arterial sampling were young, both 21 yrs (Table 1), and it is known that CBF decreases with age if no correction for partial volume effects is made [31]. However, in the present study K1 was found to be on average 30% (SD 6%) smaller in the AD- than in the HC group in the cortical regions, whereas in [29] the difference in CBF between subjects in the range of 19–46 yrs versus 60–70 yrs has been found to be only 13%.
In a previous study [4] similar K1 values were obtained in cortical areas for the AD patients (0.22±min-1) as in the present study (cf. Table 2). It should be observed that K1 was estimated using the same kinetic model (input-4k) in the two investigations. In contrast, considerably higher K1 values were obtained in the cortical areas for the HC group in the present study than in the previous one (0.32±0.05 min-1 compared to 0.22±0.04 min-1). In the present study the difference in K1 between the HC- and AD groups was around 60%. The corresponding value in [4] was only around 14%. Further, the clear difference in K1 between the HC- and AD groups for the cerebellum obtained in the present study (cf. Table 2) was not observed in [4] (0.29±0.06 min-1 for the HC group and 0.28±0.04 min-1 for the AD group). Also in other studies [32, 33] no difference in CBF was found between controls and AD patients in the cerebellum. The higher K1 values obtained for the HC group in the present study compared to the previous one could at least partly be explained as an age effect (see above), but, again, it is well known from previous studies [28] that CBF is lower in AD patients than in HC subjects, and therefore K1 is expected to be higher in the HC subjects than in the AD patients. No correction for partial volume effects (PVE) was performed in this study. Therefore the observed discrepancy in K1 between the HC- and AD groups in the cerebellum could at least partly be due to spill-over from white matter, which showed a large difference in K1 between these groups (Table 2).
Based on the uptake of PIB in the frontal cortex, the AD sample was arbitrarily divided into AD-Hi and AD-Lo groups. The K1 values in the two groups were similar, which means that no difference in CBF was detected between patients with high and low PIB accumulation. The patients in the AD-Hi group showed lower MMSE scores than those in the AD-Lo group (see Table 1). For the latter group the MMSE score was only slightly below normal and at follow-up this group of patients did not deteriorate in cognitive function [7]. Larger samples of AD patients are needed to further investigate a possible uncoupling between CBF and Aβ deposition. From the present results we cannot conclude that PIB has better sensitivity than CBF for early detection of AD (but clearly the corresponding specificity should be much better).
CONCLUSIONS
The high values of the rate constant K1 for unidirectional influx of PIB across the BBB and the correlation between changes of this parameter and changes of CBF indicate that PIB, besides imaging of Aβ deposition, also may provide an index of CBF. The net accumulation rate constant Kacc obtained from an irreversible two-compartment model gave a better contrast in cortical areas between the HC- and AD-Hi groups than the late uptake ratio, but the latter measure was found to be relatively insensitive to CBF changes. Although most patients showed clearly enhanced cortical net accumulation of PIB, there were some few patients that could not be distinguished from the control regarding PIB accumulation. On the average K1 was found to be clearly lower in the AD- than in the control group. No difference in K1 was detected between patients with high and low cortical net accumulation of PIB, suggesting that K1 provides extra valuable information besides Kacc.
CONFLICT OF INTEREST
Anna Ringheim, Anders Wall, Bengt Långström, Gunnar Antoni, Pernilla Frändberg and Sergio Estrada are employed by Uppsala Imanet GE HealthCare, Uppsala, Sweden. The dementia program within Imanet, which this manuscript is a part of, has been driven since the start as an academic program and the employees have no financial benefit of the work. None of the other authors have any conflict of interest.
APPENDIX
The time course of the regional radioactivity concentration in the tissue, Ctiss(t), was estimated from the time courses of the measured tracer concentrations in the camera Cobs(t) and in arterial whole blood Cblo(t) with the aid of the relation:
In this study CBV (dimensionless) was not measured. Owing to the rapid uptake of PIB in the brain the component of radioactivity remaining in the blood vessels could not be accurately estimated from the measured time activity in the camera, but for the same reason this component was of minor importance. Therefore, fixed regional values of CBV taken from the literature were used (Table 3).
For the experiments with arterial sampling, kinetic models requiring input functions were applied. The Gjedde–Patlak analysis [17, 18] provides a slope value that is a measure of the net accumulation rate constant (dimension: time-1). Further the common two-compartment model with input function Cinp(t) was applied. The operational equations for this model are:
This “input-4k model” contains two reversible compartments (e. g. free and bound) with concentrations CF(t) and CB(t) respectively, and four rate constants. By setting the rate constant for dissociation k4 to zero the “input-3k model” with irreversible binding of the tracer is obtained.
In principle the rate constant for binding k3 (dimension: time-1) is the parameter of primary interest, because k3 is expected to be directly proportional to the density of the PIB binding sites and therefore a suitable index of binding. An alternative index is the macro parameter , the “net accumulation rate constant, which is more robust against measurement errors. Maps of Kacc and K1 were constructed using a linear algorithm [34].
Clearly there is a positive relationship between the accumulation rate of PIB and the ratio
calculated in a late time interval. Here Ctisstar and Ctissref are the tissue concentrations of radioactivity in a target and the reference region, respectively. This “late uptake ratio” is a simple index of PIB accumulation that does not require arterial sampling or fitting of parameters and does not rest on any particular kinetic model, but utilizes the fact that increased accumulation of tracer implies increased retention at late times. Of course the results are strongly dependent on the used time interval. In this work the time interval 40–60 min was chosen. The utility of this method, rest on the assumption that the accumulation rate in the reference tissue (cerebellum) is the same in the groups examined. The measure has been used in previous studies of PIB uptake [5, 7].
ACKNOWLEDGEMENTS
This work was conducted in collaboration with Imanet, GE Healthcare. Financial support from the Swedish Research Council (project 05817, A.N.), the foundation for Old Servants (A.N.), Stohne´s foundation (A.N.), the KI foundations (A.N.), the Alzheimer Foundation in Sweden (A.N.), Swedish Brain Power (A.N., B.L.) and the EC-FP5-project NCI-MCI, QLK6-CT-2000-00502 (A.N.) is gratefully acknowledged. The Ethics committee of Uppsala University (permissions 01-340 and 02-254), the Karolinska Institute and the Isotope Committee at Uppsala Academic Hospital approved the study. The experiments comply with current laws in Sweden.


